题目内容
车从静止开始以1m/s2的加速度前进,在车开始运动的同时,车后20m处某人骑自行车开始以6m/s的速度匀速追车,能否追上?人与车的最小的距离是多少?
分析:车做匀加速运动,自行车做匀速运动,当自行车的速度与车的速度相等时,若自行车没有追上车,则就追不上车.根据速度公式,求出两车速度相等所经历的时间,由位移公式求出两车的位移,判断自行车能否追上车.当两车的速度相等时,相距最小.由位移公式求解最小距离.
解答:解:设车的速度与自行车的速度相等时所经历的时间为t0,则 v自=at0,
解得:t0=
=
s=6s,
在t0=6s内,车的位移:x车=
a
=
×1×62m=18m,
而自行车的位移:x自=v自t=6×6m=36m
二者位移之差:△x=18m<20m,所以自行车追不上车.
当二者速度相等时,距离最短,
即最短距离为:smin=x车+20m-x自=18m+20m-36m=2m.
答:人骑自行车追不上出租车,两者相距最短距离是2m.
解得:t0=
| v自 |
| a |
| 6 |
| 1 |
在t0=6s内,车的位移:x车=
| 1 |
| 2 |
| t | 2 0 |
| 1 |
| 2 |
而自行车的位移:x自=v自t=6×6m=36m
二者位移之差:△x=18m<20m,所以自行车追不上车.
当二者速度相等时,距离最短,
即最短距离为:smin=x车+20m-x自=18m+20m-36m=2m.
答:人骑自行车追不上出租车,两者相距最短距离是2m.
点评:本题是追及问题,关键要寻找两车之间的关系,抓住隐含的临界条件:速度相等是关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
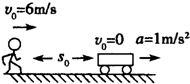 车从静止开始以1m/s2的加速度前进,车后相距s0=25m处,与车运动方向相同的人同时开始以6m/s的速度匀速追车,试通过计算说明能否追上.(要有详细计算过程)
车从静止开始以1m/s2的加速度前进,车后相距s0=25m处,与车运动方向相同的人同时开始以6m/s的速度匀速追车,试通过计算说明能否追上.(要有详细计算过程)