题目内容
在平直公路上有甲、乙两辆车在同一地点向同一方向运动,甲车以10m/s的速度做匀速直线运动,乙车从静止开始以1m/s2的加速度作匀加速直线运动,问:
(1)、甲、乙两车出发后何时再次相遇?
(2)、在再次相遇前两车何时相距最远?最远距离是多少?
(1)、甲、乙两车出发后何时再次相遇?
(2)、在再次相遇前两车何时相距最远?最远距离是多少?
分析:(1)当甲乙两车再次相遇时,位移相等,根据位移关系,结合运动学中的位移公式求出再次相遇的时间.
(2)两车速度相等之前,甲车的速度大于乙车的速度,两车之间的距离逐渐增大,两车的速度相等之后,甲车的速度小于乙车的速度,两车之间的距离逐渐减小,当两车的速度相等时,两车之间的距离最远.根据速度相等,求出时间,再根据位移公式求出相距的最远距离.
(2)两车速度相等之前,甲车的速度大于乙车的速度,两车之间的距离逐渐增大,两车的速度相等之后,甲车的速度小于乙车的速度,两车之间的距离逐渐减小,当两车的速度相等时,两车之间的距离最远.根据速度相等,求出时间,再根据位移公式求出相距的最远距离.
解答:解:(1)设经过t时间再次相遇.
此时甲车的位移x1=v1t=10t
乙车的位移x2=
at2
再次相遇时位移相等,
at2=vt,代入数据得,t=20s.
故两车经过20s再次相遇.
(2)当两车速度相等时,相距最远.
有v=at′,则t′=
=10s
此时甲车的位移x1′=vt′=10×10m=100m
乙车的位移x2′=
at′2=
×1×100m=50m
两车相距的最远距离△x=x1′-x2′=100-50m=50m.
故两车经过10s相距最远,最远距离为50m.
此时甲车的位移x1=v1t=10t
乙车的位移x2=
| 1 |
| 2 |
再次相遇时位移相等,
| 1 |
| 2 |
故两车经过20s再次相遇.
(2)当两车速度相等时,相距最远.
有v=at′,则t′=
| v |
| a |
此时甲车的位移x1′=vt′=10×10m=100m
乙车的位移x2′=
| 1 |
| 2 |
| 1 |
| 2 |
两车相距的最远距离△x=x1′-x2′=100-50m=50m.
故两车经过10s相距最远,最远距离为50m.
点评:解决本题的关键知道甲乙两车再次相遇时,位移相等.当两车速度相等时,相距最远.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
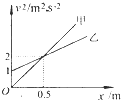 在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( )
在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( )| A、甲车的加速度比乙车的加速度小 | B、在x=0.5m处甲乙两车相遇 | C、在x=1m处甲乙两车相遇 | D、在t=2s末甲乙两车相遇 |
 在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们的运动速度的平方随位移的变化图象如图所示,则以下说法正确的是( )
在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们的运动速度的平方随位移的变化图象如图所示,则以下说法正确的是( )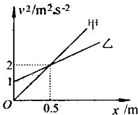 在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( )
在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( ) (2013?江苏一模)在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( )
(2013?江苏一模)在平直公路上有甲、乙两辆汽车同时从同一位置沿着同一方向做匀加速直线运动,它们速度的平方随位移变化的图象如图所示,则( )