题目内容
如图所示,在光滑的水平面上静止放一质量为m的木板B,木板表面光滑,左端固定一轻质弹簧.质量为2m的木块A以速度v0从板的右端水平向左滑上木板B.在 木块A与弹簧相互作用的过程中,下列判断正确的是( )
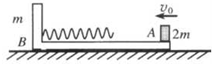

分析:滑块与木板发生弹性碰撞,动量守恒,机械能也守恒,根据守恒定律列出两个方程后联立求解;当滑块与长木板速度相等时,弹簧的压缩量最大.
解答:解:A、滑块与木板发生弹性碰撞,动量守恒;当滑块与长木板速度相等时,弹簧的压缩量最大;
此后弹簧要恢复原状,木板进一步加速,故A错误;
B、滑块与木板发生弹性碰撞,弹簧压缩量先增加后减小,故B板的加速度先增加后减小,故B错误;
C、滑块与木板发生弹性碰撞,动量守恒,机械能也守恒;
根据动量守恒定律,有:2mv0=2mv1+mv2 ①
根据机械能守恒定律,有:
?2m?
=
?2m?
+
m
②
解得:v1=
v0,v2=
v0
对滑块A,根据动量定理,有:I=2mv1-2mv0=-
mv0(负号表示方向向右)
故C错误;
D、当滑块与长木板速度相等时,弹簧的压缩量最大;
根据动量守恒定律,有:2mv0=(m+2m)v ③
系统机械能守恒,根据守恒定律,有:Ep=
?2m?
-
?(2m+m)?v2 ④
由③④两式解得:Ep=
m
,故D正确;
故选D.
此后弹簧要恢复原状,木板进一步加速,故A错误;
B、滑块与木板发生弹性碰撞,弹簧压缩量先增加后减小,故B板的加速度先增加后减小,故B错误;
C、滑块与木板发生弹性碰撞,动量守恒,机械能也守恒;
根据动量守恒定律,有:2mv0=2mv1+mv2 ①
根据机械能守恒定律,有:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
解得:v1=
| 1 |
| 3 |
| 4 |
| 3 |
对滑块A,根据动量定理,有:I=2mv1-2mv0=-
| 4 |
| 3 |
故C错误;
D、当滑块与长木板速度相等时,弹簧的压缩量最大;
根据动量守恒定律,有:2mv0=(m+2m)v ③
系统机械能守恒,根据守恒定律,有:Ep=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
由③④两式解得:Ep=
| 1 |
| 3 |
| v | 2 0 |
故选D.
点评:本题关键明确系统的运动规律,然后多次运用动量守恒定律和机械能守恒定律列式求解.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( )
如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
