题目内容
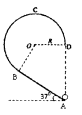
（12分）如图所示，带等量异种电荷的两平行金属板竖直放置（M板带正电，N板带负电），板间距为d=80cm，板长为L，板间电压为U=100V。两极板上边缘连线的中点处有一用水平轻质绝缘细线拴接的完全相同的小球A和B组成的装置Q，在外力作用下Q处于静止状态，该装置中两球之间有一处于压缩状态的绝缘轻质小弹簧（球与弹簧不拴接），左边A球带正电，电荷量为q=4×10-5C，右边B球不带电，两球质量均为m=1.0×10-3kg，某时刻装置Q中细线突然断裂,A、B两球立即同时获得大小相等、方向相反的速度（弹簧恢复原长）。若A、B之间弹簧被压缩时所具有的弹性能为1.0×10-3J，小球A、B均可视为质点，Q装置中弹簧的长度不计，小球带电不影响板间匀强电场，不计空气阻力，取g=10m/s2。求：
（1）为使小球不与金属板相碰，金属板长度L应满足什么条件？
（2）当小球B飞离电场恰好不与金属板相碰时，小球A飞离电场时的动能是多大？
（3）从两小球弹开进入电场开始，到两小球间水平距离为30cm时，小球A的电势能增加了多少？
(1) L<0.8m (2)8.5×10-2J (3) 5×10-4J
解析试题分析：（1）建立如图所示的直角坐标系。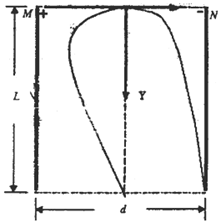
又机械能守恒定律
，得小球弹开时获得的初速度
m/s (2分)
进入电场，A球水平方向做匀减速运动，B球水平方向做匀速运动，故B碰不到极板，A球就碰不到极板。B球进入电场后向右做平抛运动，平抛时间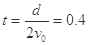
s，0.4s内的竖直位移
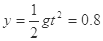m
即，为使小球不与金属板相撞，金属板长度L<0.8m (2分)
（2）水平方向上，A球向左做匀减速运动，其加速度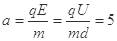
m/s2，方向向右 （1分）
当小球B恰不与金属板相撞时，A球飞离电场时沿水平方向的位移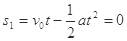
（1分）
由功能关系得A球离开电场时的动能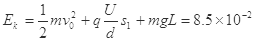
J （2分）
（3）两小球进入电场后，竖直方向均做自由落体运动，加速度为g，因此，A、B两小球在运动过程中始终位于同一条直线上，当两小球间的距离为s=30cm时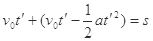
解得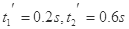
（舍去） (1分)
此时A球水平位移为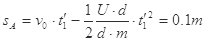
（1分）
由功能关系得A球电势能的增加量为：
J (2分)．．．
考点：本题考查带电粒子在匀强电场中的运动，应用自由落体运动和机械能守恒定律解答，该题的情景设置的较为复杂，两个过程又相互联系，在解题的过程中要理清它们之间的关系，根据运动的关系写出相应的方程来解题．
新课标阶梯阅读训练系列答案
，求：
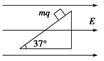
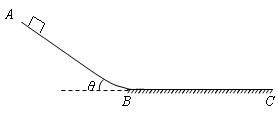
= 0.5。不计空气阻力，g =" 10" m/s2。求：
