题目内容
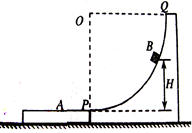
如图甲所示,平板小车A静止在水平地面上,平板板长L=6m,小物块B静止在平板左端,质量mB = 0.3kg,与A的动摩擦系数μ=0.8,在B正前方距离为S处,有一小球C,质量mC = 0.1kg,球C通过长l = 0.18m的细绳与固定点O相连,恰当选择O点的位置使得球C与物块B等高,且C始终不与平板A接触。在t = 0时刻,平板车A开始运动,运动情况满足如图乙所示SA – t关系。若BC发生碰撞,两者将粘在一起,绕O点在竖直平面内作圆周运动,并能通过O点正上方的最高点。BC可视为质点,g = 10m/s2,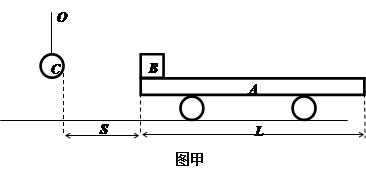

求:(1)BC碰撞瞬间,细绳拉力至少为多少?
(2)刚开始时,B与C的距离S要满足什么关系?
(1)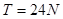 ; (2)
; (2)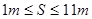
解析试题分析:平板车先做匀速直线运动后静止,在此过程中某一瞬间小物块B与C碰撞,BC碰撞后合为一体在竖直平面内做圆周运动。B与C碰撞前,B的运动情况要分类讨论:(1)B在加速阶段与C相碰;(2)B在减速阶段与C相碰
解答过程:(1)(8分)当BC恰能到达最高点时,只有重力提供向心力,则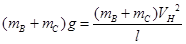 (2分)
(2分)
BC从最低点到最高点过程中,根据动能定理得: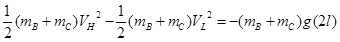 (2分)
(2分)
BC在最低点处,根据牛顿第二定律得: (2分)
(2分)
解得:T=24N (2分)
即BC碰撞瞬间,细绳拉力至少为24N
(2)(10分)BC碰撞过程中由动量守恒定律得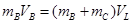 (1分)
(1分)
解得: 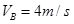
碰撞时B速度必须满足: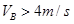 (1分)
(1分)
根据牛顿第二定律得,B的加速度为: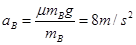 (1分)
(1分)
由图可知车A的速度为: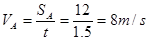 (1分)
(1分)
讨论:(1)B在加速阶段与C相碰: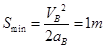 (1分)
(1分)
S要满足条件: (1分)
(1分)
(2)B在减速阶段与C相碰:
B加速阶段位移: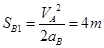 (1分)
(1分)
B加速阶段时间: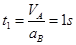 ;
;
B加速阶段A的位移: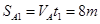 ;
;
B加速阶段AB的相对位移: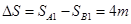 ;
;
由图可知B匀速阶段时间: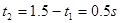 ;
;
B匀速阶段位移: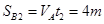 (1分)
(1分)
由图可知B匀减速阶段A速度为0
B匀减速阶段时间: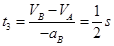
B匀减速阶段位移: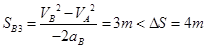 ;则物块未滑出。 (1分)
;则物块未滑出。 (1分)
B总位移: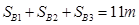
综上所述: 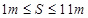 (1分)
(1分)
考点:本题考查了竖直平面内的圆周运动、动能定理、动量守恒定律,牛顿第二定律、匀变速直线运动的公式等。

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案做自由落体运动的甲、乙两物体所受的重力之比为2 : 1,下落高度之比为l: 2,则
| A.下落时间之比是1:2 |
| B.落地速度之比是1:1 |
C.落地速度之比是1: |
| D.下落过程中的加速度之比是2:1 |
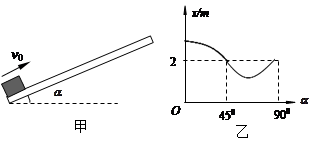
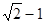

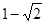
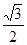
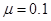 ,同时物体还要受一个随时间变化如图所示的水平拉力F的作用,设水平向左为正方向。求2s内物体的位移。
,同时物体还要受一个随时间变化如图所示的水平拉力F的作用,设水平向左为正方向。求2s内物体的位移。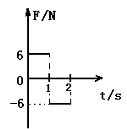
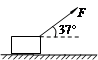

 是______
是______  ;
;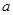 为________
为________ 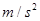 ;
;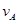 ="______"
="______" 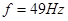 ,而做实验的同学并不知道,那么由此引起的系统误差将使加速度的测量值比实际值偏_______(填“大”或“小”).
,而做实验的同学并不知道,那么由此引起的系统误差将使加速度的测量值比实际值偏_______(填“大”或“小”).