题目内容

如图11所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界。质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90º)的方向垂直磁感线射入匀强磁场B中,第一次,粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场。第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场。不计重力的影响,粒子加速前速度认为是零,求:
小题1:为使粒子经电压U2加速射入磁场后沿直线运动,直至射出PQ边界,可在磁场区域加一匀强电场,求该电场的场强大小和方向。
小题2:加速电压
 的值。
的值。小题1:
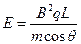
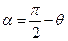
小题2:

小题1: (1)如图答1所示,经电压
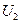 加速后以速度
加速后以速度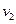 射入磁场,粒子刚好垂直PQ射出磁场,可确定粒子在磁场中做匀速圆周运动的圆心在PQ边界线的O点,半径
射入磁场,粒子刚好垂直PQ射出磁场,可确定粒子在磁场中做匀速圆周运动的圆心在PQ边界线的O点,半径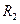 与磁场宽L的关系式为
与磁场宽L的关系式为
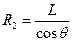 (2分),又
(2分),又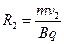 (2分),解得
(2分),解得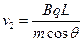 (2分)
(2分)加匀强电场后,粒子在磁场中沿直线运动射出PQ边界的条件为Eq=Bq
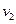 (2分),电场力的方向与磁场力的方向相反。 (2分)
(2分),电场力的方向与磁场力的方向相反。 (2分)由此可得出
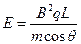 ,E的方向垂直磁场方向斜向右下(2分),与磁场边界夹角为
,E的方向垂直磁场方向斜向右下(2分),与磁场边界夹角为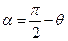 (2分),如图答2所示。
(2分),如图答2所示。小题2:
经电压
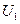 加速后粒子射入磁场后刚好不能从PQ边界射出磁场,表明在磁场中做匀速圆周运动的轨迹与PQ边界相切,要确定粒子做匀速圆周运动的圆心O的位置,如图答3所示,圆半径
加速后粒子射入磁场后刚好不能从PQ边界射出磁场,表明在磁场中做匀速圆周运动的轨迹与PQ边界相切,要确定粒子做匀速圆周运动的圆心O的位置,如图答3所示,圆半径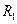 与L的关系式为:
与L的关系式为: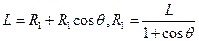 (2分)
(2分)又
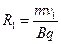 ,解得
,解得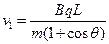 (2分)
(2分)由于
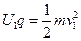 ,
,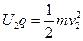 ,所以
,所以 (2分
(2分
练习册系列答案
相关题目

 A(d,0)点有一个静止的中性微粒,由于内部作用,某一时
A(d,0)点有一个静止的中性微粒,由于内部作用,某一时





 ,设
,设 =k,则k的值可能为( )
=k,则k的值可能为( ) B
B  C
C  D
D 


 cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v =
cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v = ×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.
×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件. 时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
 粒子以相同初动能沿垂直场强方向射入带电金属板间的电场中,从两板另一侧射出时[ ]
粒子以相同初动能沿垂直场强方向射入带电金属板间的电场中,从两板另一侧射出时[ ]