Question

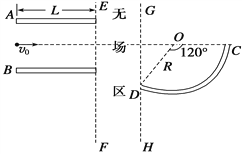
【题目】如图(a)所示，在空气中放有一半径为R、折射率为的透明球，离球心0相距R的A点处有一可向各个方向发光的点光源。求透明球表面有光射出部分的面积。提示：如图(b)所示球冠的面积公式为S=2πr(1-cosθ).空气的折射率为1.

Answer 1

【答案】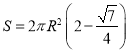

【解析】设发生全反射的临界角为C，则

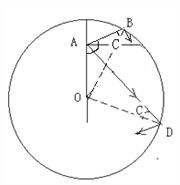
设假设光线在B点发生全反射，则由正弦定理： 解得，则α=1200，则可射出光线部分球冠所对的角度为(600-C)，cos(600-C)= ，则面积为S1=2πR[1-cos(600-C)]= ；同理在O点下方的D点也能发生全反射，可射出光线部分球冠所对的角度为(600+C)，cos(600+C)= 面积为S2=2πR[1-cos(600+C)]= .则透明球表面有光射出部分的面积为S=S1+S2=.