题目内容
3.在“用单摆测定重力加速度”的实验中,①测摆长时,若正确测出悬线长L和摆球直径d,则摆长为L+$\frac{d}{2}$;
②测周期时,当摆球经过平衡位置时开始计时并计数1次,测出经过该位置N次的时间为t,则周期为$\frac{2t}{N-1}$;
③重力加速度的表达式为g=$\frac{4{π}^{2}(N-1)^{2}(L+\frac{d}{2})}{{t}^{2}}$.
分析 ①摆线长度与摆球半径之和是单摆摆长;
②单摆完成一次全振动需要的时间是一个周期,根据题意求出周期;
③应用单摆周期公式求出重力加速度表达式.
解答 解:①摆线长度与摆球半径之和是单摆摆长,单摆摆长:l=L+$\frac{d}{2}$;
②单摆完成一次全振动需要的时间是一个周期,单摆周期:T=$\frac{t}{\frac{N-1}{2}}$=$\frac{2t}{N-1}$;
③由单摆周期公式:T=2π$\sqrt{\frac{l}{g}}$可知,重力加速度:g=$\frac{4{π}^{2}l}{{T}^{2}}$=$\frac{4{π}^{2}(N-1)^{2}(L+\frac{d}{2})}{{t}^{2}}$;
故答案为:①L+$\frac{d}{2}$;②$\frac{2t}{N-1}$;③g=$\frac{4{π}^{2}(N-1)^{2}(L+\frac{d}{2})}{{t}^{2}}$.
点评 本题考查了求摆长、周期、重力加速度问题,掌握基础知识是解题的前提,应用单摆周期公式可以解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法中正确的是( )
| A. | 电荷移动时电场力做正功,电势一定降低 | |
| B. | 电荷移动时电场力做正功,电势能一定减少 | |
| C. | 靠近正电荷处场强较大,靠近负电荷处场强较小 | |
| D. | 靠近正电荷处电势较高,靠近负电荷处电势较低 |
14. 如图所示,把一个带电小球A固定在光滑水平的绝缘桌面上,在桌面的另一处放置带电小球B,现给小球B一个垂直于AB连线方向的速度v0,使其在水平桌面上运动,则下列说法中正确的是( )
如图所示,把一个带电小球A固定在光滑水平的绝缘桌面上,在桌面的另一处放置带电小球B,现给小球B一个垂直于AB连线方向的速度v0,使其在水平桌面上运动,则下列说法中正确的是( )
 如图所示,把一个带电小球A固定在光滑水平的绝缘桌面上,在桌面的另一处放置带电小球B,现给小球B一个垂直于AB连线方向的速度v0,使其在水平桌面上运动,则下列说法中正确的是( )
如图所示,把一个带电小球A固定在光滑水平的绝缘桌面上,在桌面的另一处放置带电小球B,现给小球B一个垂直于AB连线方向的速度v0,使其在水平桌面上运动,则下列说法中正确的是( )| A. | 若A、B带同种电荷,B球一定做速度增大的曲线运动 | |
| B. | 若A、B带同种电荷,B球一定做加速度增大的曲线运动 | |
| C. | 若A、B带异种电荷,B球一定向A球运动 | |
| D. | 若A、B带异种电荷,B球可能做速度和加速度大小都不变的曲线运动 |
8. 如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
 如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )| A. | 推力F增大 | B. | 地面对小球B的弹力不变 | ||
| C. | 两个小球之间的距离减小 | D. | 竖直墙面对小球A的弹力增大 |
15.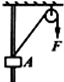 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )| A. | F不变,v不变 | B. | F增大,v减小 | C. | F增大,v增大 | D. | F增大,v不变 |
12.在做“研究平抛运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是( )
| A. | 秒表 | B. | 坐标纸 | C. | 重锤线 | D. | 弹簧秤 |
13.下列用电器中,利用静电的吸附作用进行工作的是( )
| A. | 电话机 | B. | 电冰箱 | C. | 复印机 | D. | 电饭煲 |
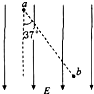 如图所示,a、b是匀强电场中的两点,质子只在电场力作用下,从a点移动到b点的过程中,电场力将做正(选填“正”或“负”)功,质子的速度将增大(选填“增大”或“减小”)
如图所示,a、b是匀强电场中的两点,质子只在电场力作用下,从a点移动到b点的过程中,电场力将做正(选填“正”或“负”)功,质子的速度将增大(选填“增大”或“减小”) 如图,一质量为m的物体B固定在轻弹簧上,弹簧下端固定在水平桌面上,弹簧原长为L.B静止时,弹簧压缩量为△L1,在B上再轻放一质量为m的物体A,A、B静止后,弹簧的弹性势能为E1;在A上施加一向下的力,使弹簧再缩短△L2,这时弹簧的弹性势能为E2.撤去向下的作用力,A、B一起向上运动.求:
如图,一质量为m的物体B固定在轻弹簧上,弹簧下端固定在水平桌面上,弹簧原长为L.B静止时,弹簧压缩量为△L1,在B上再轻放一质量为m的物体A,A、B静止后,弹簧的弹性势能为E1;在A上施加一向下的力,使弹簧再缩短△L2,这时弹簧的弹性势能为E2.撤去向下的作用力,A、B一起向上运动.求: