题目内容
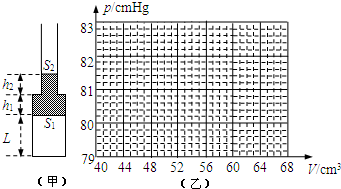
(2013?徐汇区二模)如图(甲)所示为一下粗上细且上端开口的薄壁玻璃管,管内有一部分水银封住密闭气体,上管足够长,图中大小截面积分别为S1=2cm2、S2=1cm2,粗细管内水银长度分别为h1=h2=2cm,封闭气体长度为L=22cm.大气压强为p0=76cmHg,气体初始温度为57℃.求:
(1)若缓慢升高气体温度,升高至多少开尔文方可将所有水银全部挤入细管内;
(2)若温度升高至492K,液柱下端离开玻璃管底部的距离;
(3)在图(乙)中作出全过程的p-V图象.

(1)若缓慢升高气体温度,升高至多少开尔文方可将所有水银全部挤入细管内;
(2)若温度升高至492K,液柱下端离开玻璃管底部的距离;
(3)在图(乙)中作出全过程的p-V图象.
分析:(1)根据几何关系求出水银的体积,从状态1到状态2由理想气体状态方程求解
(2)从状态2到状态3经历等压过程,列出等式求解.
(3)根据对应的压强和体积的数据作出p-V图象.
(2)从状态2到状态3经历等压过程,列出等式求解.
(3)根据对应的压强和体积的数据作出p-V图象.
解答:解:(1)由于水银总体积保持不变 设水银全部进入细管水银长度为x
V=h1S1+h2S2=xS2
x=
=6cm
P1=p0+ρg(h1+h2)=80 cmHg
P2=p0+ρgx=82 cmHg
从状态1到状态2由理想气体状态方程
=
代入数据T2=
=369K
(2)从状态2到状态3经历等压过程.
=
设水银下表面离开粗细接口处的高度为yy=
=16 cm
所以水银下表面离开玻璃管底部的距离h=y+L+h1=40 cm.
(3)根据对应的压强和体积的数据作出p-V图象.

答:(1)若缓慢升高气体温度,升高至369K方可将所有水银全部挤入细管内;
(2)若温度升高至492K,液柱下端离开玻璃管底部的距离是40 cm;
(3)如图.
V=h1S1+h2S2=xS2
x=
| h1S1+h2S2 |
| S2 |
P1=p0+ρg(h1+h2)=80 cmHg
P2=p0+ρgx=82 cmHg
从状态1到状态2由理想气体状态方程
| p1V1 |
| T1 |
| p2V2 |
| T2 |
代入数据T2=
| p2V2T1 |
| p1V1 |
(2)从状态2到状态3经历等压过程.
| V2 |
| T2 |
| V3 |
| T3 |
设水银下表面离开粗细接口处的高度为yy=
| (L+h1)T 3S1-(L+h1)T2S1 |
| T2S2 |
所以水银下表面离开玻璃管底部的距离h=y+L+h1=40 cm.
(3)根据对应的压强和体积的数据作出p-V图象.

答:(1)若缓慢升高气体温度,升高至369K方可将所有水银全部挤入细管内;
(2)若温度升高至492K,液柱下端离开玻璃管底部的距离是40 cm;
(3)如图.
点评:找出各个状态下的参量是正确解题的关键,熟练应用理想气体状态方程即可正确解题.

练习册系列答案
相关题目
 (2013?徐汇区二模)一列沿x轴正方向传播的简谐横波,波速为0.5m/s,在某时刻波形如图中实线所示,经过一段时间后波形如图中虚线所示,在这段时间内,图中P处的质点通过的路程可能是( )
(2013?徐汇区二模)一列沿x轴正方向传播的简谐横波,波速为0.5m/s,在某时刻波形如图中实线所示,经过一段时间后波形如图中虚线所示,在这段时间内,图中P处的质点通过的路程可能是( ) (2013?徐汇区二模)在光滑绝缘的水平桌面上,存在着方向水平向右的匀强电场,电场线如图中实线所示.一带正电、初速度不为零的小球从桌面上的A点开始运动,到C点时,突然受到一个外加的水平恒力F作用而继续运动到B点,其运动轨迹如图中虚线所示,v表示小球经过C点时的速度.则( )
(2013?徐汇区二模)在光滑绝缘的水平桌面上,存在着方向水平向右的匀强电场,电场线如图中实线所示.一带正电、初速度不为零的小球从桌面上的A点开始运动,到C点时,突然受到一个外加的水平恒力F作用而继续运动到B点,其运动轨迹如图中虚线所示,v表示小球经过C点时的速度.则( ) (2013?徐汇区二模)静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一质量为m、带电量为+q的粒子(不计重力),以初速度v0从O点(x=0)进入电场,沿x轴正方向运动.下列叙述正确的是( )
(2013?徐汇区二模)静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一质量为m、带电量为+q的粒子(不计重力),以初速度v0从O点(x=0)进入电场,沿x轴正方向运动.下列叙述正确的是( ) (2013?徐汇区二模)如图所示为α粒子散射实验装置,α粒子打到荧光屏上都会引起闪烁,若将带有荧光屏的显微镜分别放在图中A、B、C、D四处位置.则这四处位置在相等时间内统计的闪烁次数可能符合事实的是( )
(2013?徐汇区二模)如图所示为α粒子散射实验装置,α粒子打到荧光屏上都会引起闪烁,若将带有荧光屏的显微镜分别放在图中A、B、C、D四处位置.则这四处位置在相等时间内统计的闪烁次数可能符合事实的是( )