题目内容
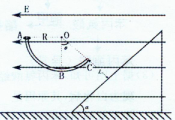
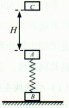
(20分)在水平方向的匀强电场中有一段表面光滑的圆形绝缘杆ABC、圆心为O点,半径为R= m, A、O两点等高,C、O两点的连线与竖直方向成θ=45°角C点到斜面的距离L=
m, A、O两点等高,C、O两点的连线与竖直方向成θ=45°角C点到斜面的距离L= m,斜面倾角为α=45°,如图所示。有一质量m=" 500" g的带负电小环套在直杆上,所受电场力的大小等于其重力大小,小环由A点静止开始沿杆下滑,飞出C点后撞上斜面某点。(已知
m,斜面倾角为α=45°,如图所示。有一质量m=" 500" g的带负电小环套在直杆上,所受电场力的大小等于其重力大小,小环由A点静止开始沿杆下滑,飞出C点后撞上斜面某点。(已知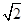 ≈1.4,g取10 m/s2)求:
≈1.4,g取10 m/s2)求:
(1)小环到C点的速度大小;
(2)小环由C点抛出到撞击斜面所经历的时间和撞击点与C点的距离。(保留两位有效数字)
 m, A、O两点等高,C、O两点的连线与竖直方向成θ=45°角C点到斜面的距离L=
m, A、O两点等高,C、O两点的连线与竖直方向成θ=45°角C点到斜面的距离L= m,斜面倾角为α=45°,如图所示。有一质量m=" 500" g的带负电小环套在直杆上,所受电场力的大小等于其重力大小,小环由A点静止开始沿杆下滑,飞出C点后撞上斜面某点。(已知
m,斜面倾角为α=45°,如图所示。有一质量m=" 500" g的带负电小环套在直杆上,所受电场力的大小等于其重力大小,小环由A点静止开始沿杆下滑,飞出C点后撞上斜面某点。(已知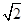 ≈1.4,g取10 m/s2)求:
≈1.4,g取10 m/s2)求:
(1)小环到C点的速度大小;
(2)小环由C点抛出到撞击斜面所经历的时间和撞击点与C点的距离。(保留两位有效数字)
解:(1)对小环进行受力分析,并根据动能定理, mv2=mg·
mv2=mg·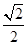 R+mg(1+
R+mg(1+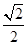 )R,
)R,
解得:小环到C点的速度大小v=4m/s。
(2)小环通过C点后做类平抛运动,平行斜面方向做匀速直线运动,垂直斜面方向做初速度为零的匀加速直线运动,加速度a=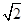 g,
g,
由L= at2,解得飞行时间t=0.20s。
at2,解得飞行时间t=0.20s。
x=vt=0.8m。
撞击点与C点的距离s=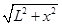 =0.84m。
=0.84m。
 mv2=mg·
mv2=mg·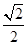 R+mg(1+
R+mg(1+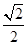 )R,
)R,解得:小环到C点的速度大小v=4m/s。
(2)小环通过C点后做类平抛运动,平行斜面方向做匀速直线运动,垂直斜面方向做初速度为零的匀加速直线运动,加速度a=
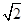 g,
g,由L=
 at2,解得飞行时间t=0.20s。
at2,解得飞行时间t=0.20s。x=vt=0.8m。
撞击点与C点的距离s=
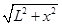 =0.84m。
=0.84m。应用动能定理和类平抛运动规律及其相关知识解答。

练习册系列答案
相关题目
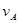 ,小球B运动的速度大小为
,小球B运动的速度大小为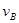 ,轻绳与杆的夹角为
,轻绳与杆的夹角为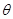 .则( )
.则( )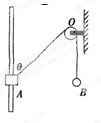
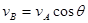
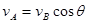
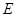 ,在电场中
,在电场中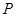 处由静止下落一质量为
处由静止下落一质量为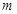 、带电量为
、带电量为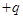 的小球(可视为质点)。在
的小球(可视为质点)。在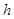 处有一水平弹性绝缘挡板
处有一水平弹性绝缘挡板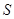 (挡板不影响电场的分布),小球每次与挡板相碰后电量减小到碰前的
(挡板不影响电场的分布),小球每次与挡板相碰后电量减小到碰前的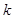 倍(
倍(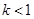 ),而碰撞过程中小球的机械能不损失,即碰撞前后小球的速度大小不变,方向相反。设在匀强电场中,挡板
),而碰撞过程中小球的机械能不损失,即碰撞前后小球的速度大小不变,方向相反。设在匀强电场中,挡板
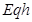
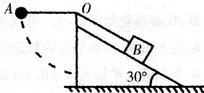
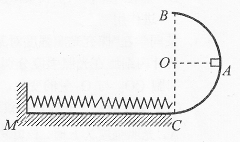
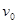 滑上放在光滑水平面上的长木板B,若B固定,则A恰好滑到B的右端时停下,若B不固定,则A在B上滑行的长度为木板长的
滑上放在光滑水平面上的长木板B,若B固定,则A恰好滑到B的右端时停下,若B不固定,则A在B上滑行的长度为木板长的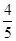 ,求A和B的质量
,求A和B的质量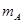 与
与 之比。
之比。
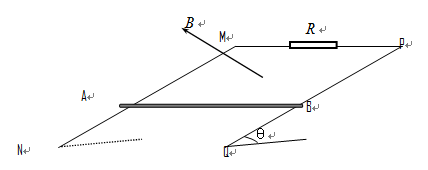
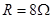 的电阻;导轨间距为
的电阻;导轨间距为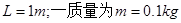 ,电阻
,电阻 ,长约
,长约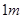 的均匀金属杆水平放置在导轨上,它与导轨的滑动摩擦因数
的均匀金属杆水平放置在导轨上,它与导轨的滑动摩擦因数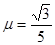 ,导轨平面的倾角为
,导轨平面的倾角为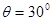 在垂直导轨平面方向有匀强磁场,磁感应强度为
在垂直导轨平面方向有匀强磁场,磁感应强度为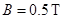 ,今让金属杆AB由静止开始下滑从杆静止开始到杆AB恰好匀速运动的过程中经过杆的电量
,今让金属杆AB由静止开始下滑从杆静止开始到杆AB恰好匀速运动的过程中经过杆的电量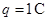 ,求:
,求: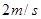 时加速度的大小
时加速度的大小