题目内容
一辆摩托车从静止出发做匀加速直线运动,追赶前方300m处正以20m/s的速度匀速前进的汽车,已知摩托车速度达到30m/s后匀速运动,又经过80s刚好追上汽车,求:
(1)摩托车的加速度;
(2)在摩托车追上汽车前它们之间的最大距离.
(1)摩托车的加速度;
(2)在摩托车追上汽车前它们之间的最大距离.
分析:(1)设摩托车的加速度为a,加速到速度为30m/s时时间为t1,画出它们的v-t图象,摩托车和汽车相遇时两者的位移相等,从图象上可看出两者的面积相等,根据速度、位移关系列式即可求解;
(2)速度相等时距离最大,由此可得时间,进而算出最大距离.
(2)速度相等时距离最大,由此可得时间,进而算出最大距离.
解答: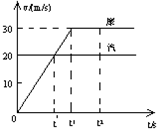 解:(1)设摩托车的加速度为a,加速到速度为30m/s时时间为t1,画出它们的v-t图象,如图所示:
解:(1)设摩托车的加速度为a,加速到速度为30m/s时时间为t1,画出它们的v-t图象,如图所示:
则:t1=
…①
△t=80s
t2=t1+△t=80+
…②
摩托车和汽车相遇时两者的位移相等,从图象上可看出两者的面积相等.则:s=
×30×t1+30×80=20t2+300…③
把①②式代入③得:
×30×
+30×80=20×(80+
)+300
解得:a=0.30m/s2
(2)从图象上可看出,当摩托车速度达到20m/s时,两车相距最大,则:t/=
=
=66.67s
此时有:△s=(
×20×
+300)m=966.67m
在摩托车追上汽车前它们之间的最大距离为966.67m.
答:(1)摩托车的加速度为0.30m/s2;
(2)在摩托车追上汽车前它们之间的最大距离为966.67m.
 解:(1)设摩托车的加速度为a,加速到速度为30m/s时时间为t1,画出它们的v-t图象,如图所示:
解:(1)设摩托车的加速度为a,加速到速度为30m/s时时间为t1,画出它们的v-t图象,如图所示:则:t1=
| 30 |
| a |
△t=80s
t2=t1+△t=80+
| 30 |
| a |
摩托车和汽车相遇时两者的位移相等,从图象上可看出两者的面积相等.则:s=
| 1 |
| 2 |
把①②式代入③得:
| 1 |
| 2 |
| 30 |
| a |
| 30 |
| a |
解得:a=0.30m/s2
(2)从图象上可看出,当摩托车速度达到20m/s时,两车相距最大,则:t/=
| △v |
| a |
| 20 |
| 0.30 |
此时有:△s=(
| 1 |
| 2 |
| 20 |
| 0.30 |
在摩托车追上汽车前它们之间的最大距离为966.67m.
答:(1)摩托车的加速度为0.30m/s2;
(2)在摩托车追上汽车前它们之间的最大距离为966.67m.
点评:本题重点是在第一问,这里必须要弄清楚,在追上前,摩托车是不是达到了最大速度,忽略这一问题,本题一定出错.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目