题目内容
(1)如图1所示,沿波的传播方向上有间距均为1m的6个质点a、b、c、d、e、f,它们均静止在各自的平衡位置.一列横波以1m/s的速度水平向右传播,t=0时到达质点a,质点a开始由平衡位置向上运动.t=1s时,质点a第一次到达最高点,则在4s<t<5s这段时间内:
A.质点c的加速度逐渐增大 B.质点a的速度逐渐增大
C.质点d向下运动 D.质点f保持静
(2)如图2所示,一束光线以60°的入射角射到一水平放置的平面镜上,反射后在上方与平面镜平行的光屏上留下一光点P,现在将一块上下两面平行的透明体平放在平面镜上,则进入透明体的光线经平面镜反射后再从透明体的上表面射出,打在光屏上的P′点,与原来相比向左平移了3.46cm,已知透明体对光的折射率为
 .求光在透明体里运动的时间多长?
.求光在透明体里运动的时间多长?
【答案】分析:(1)由题,质点a开始由平衡位置向上运动,t=1s时,质点a第一次到达最高点,求出周期,再求出波长.根据波的形成过程,分析在4s<t<5s这段时间内各个质点的位置和运动方向,判断速度和加速度如何变化.
(2)作出光路图.根据折射定律求出光线在透明体上表面的折射角,由几何知识求出光在透明体内传播的路程.由v=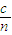 求出光在透明体内传播速度,再求出光在透明体里运动的时间.
求出光在透明体内传播速度,再求出光在透明体里运动的时间.
解答:解:(1)由题得到波的周期为T=4s,波长为λ=vT=4m,各个质点起振方向均向上.
A、波从a传到c的时间为2s,则在4s<t<5s这段时间内,c正从平衡位置向波谷运动,加速度增大.故A正确.
B、在4s<t<5s这段时间内,a正从平衡位置向波峰运动,速度减小.故B错误.
C、波从a传到d的时间为3s,在4s<t<5s这段时间内,d正从波峰向平衡位置运动,即向下运动.故C正确.
D、在4s<t<5s这段时间内,波还没有传到f,质点f保持静.故D正确.
故选ACD
(2)光路图如图所示.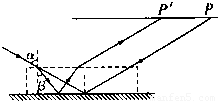 已知入射角α=60°,折射率n=
已知入射角α=60°,折射率n=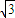 ,由折射定律n=
,由折射定律n=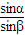 得,折射角β=30°.
得,折射角β=30°.
设透明体的厚度为d,由题意及光路图得△s=2dtan60°-2dtan30°,代入数值解得d=1.5 cm.
光在透明介质里传播的速度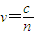 ,
,
光在透明介质里的路程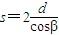 ,
,
所以光在透明体里运动的时间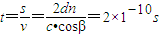
答:
(1)ACD;
(2)光在透明体里运动的时间为2×10-10s.
点评:对于机械波的形成过程,要抓住波的基本特点:介质中各质点的起振方向与波源的起振方向都相同.几何光学要规范地作出光路图,根据几何知识和折射定律结合研究是常用的思路.
(2)作出光路图.根据折射定律求出光线在透明体上表面的折射角,由几何知识求出光在透明体内传播的路程.由v=
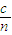 求出光在透明体内传播速度,再求出光在透明体里运动的时间.
求出光在透明体内传播速度,再求出光在透明体里运动的时间.解答:解:(1)由题得到波的周期为T=4s,波长为λ=vT=4m,各个质点起振方向均向上.
A、波从a传到c的时间为2s,则在4s<t<5s这段时间内,c正从平衡位置向波谷运动,加速度增大.故A正确.
B、在4s<t<5s这段时间内,a正从平衡位置向波峰运动,速度减小.故B错误.
C、波从a传到d的时间为3s,在4s<t<5s这段时间内,d正从波峰向平衡位置运动,即向下运动.故C正确.
D、在4s<t<5s这段时间内,波还没有传到f,质点f保持静.故D正确.
故选ACD
(2)光路图如图所示.
 已知入射角α=60°,折射率n=
已知入射角α=60°,折射率n=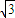 ,由折射定律n=
,由折射定律n=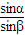 得,折射角β=30°.
得,折射角β=30°.设透明体的厚度为d,由题意及光路图得△s=2dtan60°-2dtan30°,代入数值解得d=1.5 cm.
光在透明介质里传播的速度
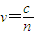 ,
,光在透明介质里的路程
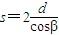 ,
,所以光在透明体里运动的时间
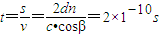
答:
(1)ACD;
(2)光在透明体里运动的时间为2×10-10s.
点评:对于机械波的形成过程,要抓住波的基本特点:介质中各质点的起振方向与波源的起振方向都相同.几何光学要规范地作出光路图,根据几何知识和折射定律结合研究是常用的思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (1)如图1所示,一细束复色光(含红、蓝两种单色光)沿PO射向半圆形玻璃砖圆心O,观察到反射光线和折射光线分别为OQ、OR.下列判断不正确的是
(1)如图1所示,一细束复色光(含红、蓝两种单色光)沿PO射向半圆形玻璃砖圆心O,观察到反射光线和折射光线分别为OQ、OR.下列判断不正确的是
