题目内容
4.2013年12月2日,我国探月卫星“嫦娥三号”成功发射,“嫦娥三号”最终进入距月面h=200km的圆形工作轨道,开始进行科学探测活动,设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列说法正确的是( )| A. | 嫦娥三号绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| B. | 月球的平均密度为$\frac{3g}{4πGR}$ | |
| C. | 嫦娥三号在工作轨道上的绕行速度为$\sqrt{g(R+h)}$ | |
| D. | 在嫦娥三号的工作轨道处的重力加速度为$\frac{GM}{(R+h)}$ |
分析 根据万有引力提供向心力及GM=gR2求周期、线速度和加速度.
可根据GM=gR2,求出月球的质量,从而求出月球的密度.
解答 解:A、根据万有引力提供向心力,有:G$\frac{Mm}{{(R+h)}^{2}}$=m$\frac{{4π}^{2}(R+h)}{{T}^{2}}$及GM=gR2
解得:T=2π$\sqrt{\frac{{(R+h)}^{3}}{{gR}^{2}}}$,故A错误
B、根据万有引力等于重力得GM=gR2,月球的质量为$\frac{g{R}^{2}}{G}$,月球的密度ρ=$\frac{M}{V}$=$\frac{3g}{4πGR}$,故B正确;
C、根据圆周运动知识得:v=$\frac{2π(R+h)}{T}$=$\sqrt{\frac{{gR}^{2}}{R+h}}$,故B错误
D、根据万有引力提供向心力G$\frac{Mm}{{(R+h)}^{2}}$=ma,所以:a=$G\frac{M}{{(R+h)}^{2}}$ 故D错误.
故选:B.
点评 解决本题的关键掌握万有引力提供向心力公式,要注意黄金代换式的应用,难度适中.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
13. 理想实验有时更能反映自然规律.伽利略设计了一个理想实验:
理想实验有时更能反映自然规律.伽利略设计了一个理想实验:
①减小另一个斜面的倾角,小球在这个斜面上仍能达到原来的高度
②两个斜面对接,让静止小球沿一个斜面滚下,小球将滚上另一个斜面
③如果没有摩擦,小球将上升到原来释放时的高度
④继续减小第二个斜面的倾角,最后使它成为水平面,小球要沿水平面做持续的匀速运
关于该实验下列说法正确的是( )
 理想实验有时更能反映自然规律.伽利略设计了一个理想实验:
理想实验有时更能反映自然规律.伽利略设计了一个理想实验:①减小另一个斜面的倾角,小球在这个斜面上仍能达到原来的高度
②两个斜面对接,让静止小球沿一个斜面滚下,小球将滚上另一个斜面
③如果没有摩擦,小球将上升到原来释放时的高度
④继续减小第二个斜面的倾角,最后使它成为水平面,小球要沿水平面做持续的匀速运
关于该实验下列说法正确的是( )
| A. | ①是事实,②③④是推论 | B. | ②是事实,①③④是推论 | ||
| C. | ③是事实,①②④是推论 | D. | ④是事实,①②③是推论 |
14.关于单位制,下列说法中正确的是( )
| A. | kg、m/s、N是导出单位 | |
| B. | kg、m、C是基本单位 | |
| C. | 在国际单位制中,时间的单位是s,属基本单位 | |
| D. | 在国际单位制中,力的单位是根据牛顿第二定律定义的 |
 M=2千克的均匀木板长为L=40cm,放在水平面上,右端与桌面齐,板与桌面间的摩擦系数为μ=0.2现用水平力将其推落,水平力至少做功为0.8J.
M=2千克的均匀木板长为L=40cm,放在水平面上,右端与桌面齐,板与桌面间的摩擦系数为μ=0.2现用水平力将其推落,水平力至少做功为0.8J.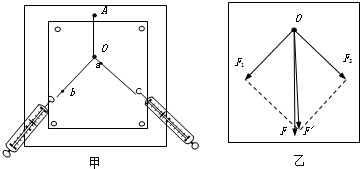 如图甲所示,在“验证力的平行四边形定则”的实验中,某同学进行实验的主要步骤是:将橡皮筋的一端固定在木板上的A点,另一端拴上两根绳套,每根绳套分别连着一个弹簧测力计.沿着两个方向拉弹簧测力计,将橡皮筋的活动端拉到某一位置,将此位置标记为O点,读取此时弹簧测力计的示数,分别记录两个拉力F1、F2的大小.再用笔在两绳的拉力方向上分别标记a、b两点,并分别将其与O点连接,表示两力的方向.再用一个弹簧测力计将橡皮筋的活动端仍拉至O点,记录其拉力F的大小并用上述方法记录其方向.
如图甲所示,在“验证力的平行四边形定则”的实验中,某同学进行实验的主要步骤是:将橡皮筋的一端固定在木板上的A点,另一端拴上两根绳套,每根绳套分别连着一个弹簧测力计.沿着两个方向拉弹簧测力计,将橡皮筋的活动端拉到某一位置,将此位置标记为O点,读取此时弹簧测力计的示数,分别记录两个拉力F1、F2的大小.再用笔在两绳的拉力方向上分别标记a、b两点,并分别将其与O点连接,表示两力的方向.再用一个弹簧测力计将橡皮筋的活动端仍拉至O点,记录其拉力F的大小并用上述方法记录其方向.

 如图所示,电源电动势、内电阻、R1、R2均未知,当a、b间接入电阻R1′=10Ω时,电流表示数为I1=1A;当接入电阻R2′=18Ω时,电流表示数为I2=0.6A.当a、b间接入电阻R3′=118Ω时,电流表示数为多少?
如图所示,电源电动势、内电阻、R1、R2均未知,当a、b间接入电阻R1′=10Ω时,电流表示数为I1=1A;当接入电阻R2′=18Ω时,电流表示数为I2=0.6A.当a、b间接入电阻R3′=118Ω时,电流表示数为多少?