题目内容
19.用如图1实验装置验证m1、m2组成的系统机械能守恒.m2从高处由静止开始下落,m1上拖着的纸带打出一系列的点,对纸带上的点迹进行测量,即可验证机械能守恒定律.图2给出的是实验中获取的一条纸带:0是打下的第一个点,每相邻两计数点间还有4个点(图中未标出),计数点间的距离如图2所示.已知m1=50g、m2=150g,则(g取10m/s2,结果保留两位有效数字)
(1)在纸带上打下记数点5时的速度v=2.4m/s;
(2)在打点0~5过程中系统动能的增量△EK=0.58J,系统势能的减少量△EP=0.60J,由此得出的结论是在在误差允许的范围内,m1、m2组成的系统机械能守恒.;
(3)若某同学作出$\frac{1}{2}$v2-h图象如图3,则当地的实际重力加速度g=9.7m/s2.
分析 (1)根据在匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度,可以求出打下记数点5时的速度大小;
(2)根据物体的初末动能大小可以求出动能的增加量,根据物体重力做功和重力势能之间的关系可以求出系统重力势能的减小量,比较动能增加量和重力势能减小量之间的关系可以得出机械能是否守恒;
(3)根据图象的物理意义可知,图象的斜率大小等于物体的重力加速度大小;
解答 解:(1)由于每相邻两个计数点间还有4个点没有画出,所以相邻的计数点间的时间间隔T=0.1s,
根据在匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度,可知打第5个点时的速度为:
v5=$\frac{0.216+0.264}{2×0.1}$=2.4m/s;
(2)在0~5过程中系统动能的增量△EK=$\frac{1}{2}$(m1+m2)v52=$\frac{1}{2}$×0.2×2.42J=0.58J;
系统重力势能的减小量等于物体重力做功,故:△EP=W=(m2-m1)gx=0.1×10×(0.216+0.384)=0.60J;
由此可知动能的增加量和势能的减小量基本相等,因此在在误差允许的范围内,m1、m2组成的系统机械能守恒.
(3)根据系统机械能守恒有:(m2-m1)gh=$\frac{1}{2}$(m1+m2)v2
则$\frac{1}{2}$v2=$\frac{{{m}_{2}-m}_{1}}{{{m}_{1}+m}_{2}}$gh
知图线的斜率k=$\frac{{{m}_{2}-m}_{1}}{{{m}_{1}+m}_{2}}$g=$\frac{5.82}{1.20}$
解得g=9.7m/s2.
故答案为:(1)2.4;(2)0.58,0.60,在在误差允许的范围内,m1、m2组成的系统机械能守恒.
(3)9.7
点评 本题全面的考查了验证机械能守恒定律中的数据处理问题,要熟练掌握匀变速直线运动的规律以及功能关系,增强数据处理能力.

 53随堂测系列答案
53随堂测系列答案
| A. | 该电场可能是匀强电场 | |
| B. | 比较M、N两点的场强大小,一定有EM>EN | |
| C. | 比较同一个试探电荷在M、N两点受到的电场力,一定有FM<FN | |
| D. | 比较电子在M、N两点的电势能,一定有EM>EN |
 如图所示,电动势为E、内阻不计的电源与三个灯泡和三个电阻相接.只合上开关S1,三个灯泡都能正常工作.如果再合上S2,则下列表述正确的( )
如图所示,电动势为E、内阻不计的电源与三个灯泡和三个电阻相接.只合上开关S1,三个灯泡都能正常工作.如果再合上S2,则下列表述正确的( )| A. | 通过R1上的电流减小 | B. | L2上消耗的功率增大 | ||
| C. | 通过R3上的电流减小 | D. | 电源输出功率减小 |
 物块A1、A2、B1和B2的质量均为m,A1、A2用刚性轻杆连接,B1、B2用轻质弹簧连结,两个装置都放在水平的支托物上,处于平衡状态,如图今突然撤去支托物,让物块下落,在除去支托物的瞬间,A1、A2受到的合力分别为${F_{f_1}}$和${F_{f_2}}$,B1、B2受到的合力分别为F1和F2,则( )
物块A1、A2、B1和B2的质量均为m,A1、A2用刚性轻杆连接,B1、B2用轻质弹簧连结,两个装置都放在水平的支托物上,处于平衡状态,如图今突然撤去支托物,让物块下落,在除去支托物的瞬间,A1、A2受到的合力分别为${F_{f_1}}$和${F_{f_2}}$,B1、B2受到的合力分别为F1和F2,则( )| A. | ${F_{f_1}}$=0,${F_{f_2}}$=2mg,F1=0,F2=2mg? | |
| B. | ${F_{f_1}}$=mg,${F_{f_2}}$=mg,F1=0,F2=2mg | |
| C. | ${F_{f_1}}$=mg,${F_{f_2}}$=2mg,F1=mg,F2=mg? | |
| D. | ${F_{f_1}}$=mg,${F_{f_2}}$=mg,F1=mg,F2=mg |
| A. | 嫦娥三号绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| B. | 月球的平均密度为$\frac{3g}{4πGR}$ | |
| C. | 嫦娥三号在工作轨道上的绕行速度为$\sqrt{g(R+h)}$ | |
| D. | 在嫦娥三号的工作轨道处的重力加速度为$\frac{GM}{(R+h)}$ |
| A. | 卡文迪许巧妙地运用扭秤实验,用了放大法成功测出静电力常量的数值 | |
| B. | 牛顿为了说明力不是维持物体运动的原因用了理想实验法 | |
| C. | 在不需要考虑物体本身的形状和大小时,用质点来代替物体的方法叫假设法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加之和代表物体的位移,这里采用了微元法 |

| A. | 4Ω | B. | 16Ω | C. | 18Ω | D. | 20Ω |
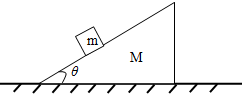 如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)若小物块在斜面上由静止开始下滑,当滑行距离s=1m时,其速度v=2m/s.在此过程中木楔没有动,求:
如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)若小物块在斜面上由静止开始下滑,当滑行距离s=1m时,其速度v=2m/s.在此过程中木楔没有动,求: 如图所示,是“研究电磁感应现象”的实验装置.
如图所示,是“研究电磁感应现象”的实验装置.