题目内容
如图所示,水平面上有两个木块,两木块的质量分别为m1、m2,且m2=2m1.开始两木块之间有一根用轻绳缚住的已压缩的轻弹簧,烧断细绳后,两木块分别向左、右运动.若两木块m1和m2与水平面间的动摩擦因数为μ1、μ2,且μ1=2μ2,则在弹簧伸长的过程中,两木块( )
| A.动量大小之比为1∶1 | B.速度大小之比为2∶1 |
| C.通过的路程之比为2∶1 | D.通过的路程之比为1∶1 |
ABC
解析试题分析:以两木块及弹簧为研究对象,绳断开后,弹簧将对两木块有推力作用,这可以看成是内力;水平面对两木块有方向相反的滑动摩擦力,且F1=μ1m1g,F2=μ2m2g.因此系统所受合外力F合=μ1m1g-μ2m2g=0,即满足动量守恒定律的条件.
设弹簧伸长过程中某一时刻,两木块速度大小分别为v1、v2.由动量守恒定律有(以向右为正方向):
-m1v1+m2v2=0,即m1v1=m2v2,即两物体的动量大小之比为1∶1,故A项正确;两物体的速度大小之比为 ,故B项正确;由于木块通过的路程正比于其速度,两木块通过的路程之比
,故B项正确;由于木块通过的路程正比于其速度,两木块通过的路程之比 ,故C项正确,D项错误。
,故C项正确,D项错误。
考点:动量守恒定律及其应用

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案如图所示,a、b和c表示电场中的三个等势面,a和c的电势分别为U和 U,a、b 的电势差等于b、c的电势差.一带电粒子从等势面a上某处以速度υ释放后,仅受电场力作用而运动,经过等势面c时的速率为2υ,则它经过等势面b时的速率为( )
U,a、b 的电势差等于b、c的电势差.一带电粒子从等势面a上某处以速度υ释放后,仅受电场力作用而运动,经过等势面c时的速率为2υ,则它经过等势面b时的速率为( )
A. υ υ | B. υ υ | C.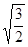 υ υ | D.1.5υ |
如图所示,固定坡道倾角为θ,顶端距光滑水平面的高度为h,一可视为质点的小物块质量为m,从坡道顶端由静止滑下,经过底端O点进入水平面时无机械能损失,为使小物块制动将轻弹簧的一端固定在水平面左侧M处的竖直墙上,弹簧自由伸长时右侧一端恰好位于O点,已知小物块与坡道间的动摩擦因数为 ,重力加速度为g,则下列说法正确的是( )
,重力加速度为g,则下列说法正确的是( )
| A.小物块在倾斜轨道上运动时,下滑的加速度比上滑的加速度小 |
| B.当小物块压缩弹簧到最短时,物块的重力势能完全转化为弹簧的弹性势能 |
C.小物块返回倾斜轨道时所能达到的最大高度为 |
| D.小物块在往返运动的整个过程中损失的机械能为mgh |
如图所示的电场中,虚线为某带电粒子只在电场力作用下的运动轨迹,a、b、c是轨迹上的三个点,则
| A.粒子一定带正电 |
| B.粒子一定是从a点运动到b点 |
| C.粒子在c点加速度一定大于在b点加速度 |
| D.粒子在电场中c点的电势能一定小于在b点的电势能 |
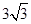 m/s平抛救生圈,第一个刚落到快艇,接着抛第二个,结果第二个救生圈刚好与甲队员同时抵达快艇,若人的质量m,重力加速度g=10m/s2,问:
m/s平抛救生圈,第一个刚落到快艇,接着抛第二个,结果第二个救生圈刚好与甲队员同时抵达快艇,若人的质量m,重力加速度g=10m/s2,问:

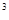 kg,发动机的额定功率为60kW,汽车所受阻力恒为2000N,如果汽车从静止开始以2m/s
kg,发动机的额定功率为60kW,汽车所受阻力恒为2000N,如果汽车从静止开始以2m/s 的加速度做匀加速直线运动,功率达到最大后汽车又以额定功率运动了一段距离达到了最大速度,在整个过程中汽车运动了100m。下面是甲、乙两位同学关于此过程中汽车牵引力做功的解法:
的加速度做匀加速直线运动,功率达到最大后汽车又以额定功率运动了一段距离达到了最大速度,在整个过程中汽车运动了100m。下面是甲、乙两位同学关于此过程中汽车牵引力做功的解法: ①
① ×10J=6×10
×10J=6×10 J ②
J ② J ④
J ④ ,质量之比为
,质量之比为 ,若两车与路面的动摩擦因数相同,且不计空气阻力,当汽车急刹车后,甲、乙两车滑行的最大距离S1和S2之比是
,若两车与路面的动摩擦因数相同,且不计空气阻力,当汽车急刹车后,甲、乙两车滑行的最大距离S1和S2之比是


