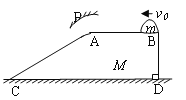
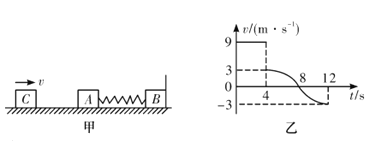
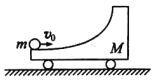
题目内容
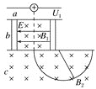
【题目】质谱仪原理如图所示,a为粒子加速器,电压为U1;b为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;c为偏转分离器,磁感应强度为B2.今有一质量为m、电荷量为e的正粒子(不计重力),经加速后,该粒子恰能通过速度选择器,粒子进入分离器后做匀速圆周运动.求:
(1)粒子的速度v为多少?
(2)速度选择器的电压U2为多少?
(3)粒子在B2磁场中做匀速圆周运动的半径R为多大?
【答案】(1) ![]() (2)B1d
(2)B1d ![]() (3)
(3) ![]()
![]()
【解析】
解: (1)在电场中,粒子被加速电场U1加速,由动能定理有:![]()
解得粒子的速度:![]()
(2)在速度选择器中,粒子受的电场力和洛伦兹力大小相等,则有:![]()
解得速度选择器的电压:![]()
(3)在磁场中,粒子受洛伦兹力作用而做圆周运动,则有:![]()
解得半径:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目