题目内容
8．物体由静止开始做加速度为2m/s2的匀加速直线运动，当速度达到v时，改为加速度大小为3m/s2的匀减速直线运动，直至速度减为0，则在匀加速和匀减速过程中物体经过的位移之比为3：2，两过程所用的时间之比为3：2，平均速度之比为1：1．分析 根据匀变速直线运动的速度位移公式求出经过的位移之比．根据速度时间公式求出两过程运动的时之比，根据平均速度推论求出平均速度之比．
解答 解：根据x=$\frac{{v}^{2}}{2a}$知，匀加速和匀减速运动的加速度大小之比为2：3，则匀加速和匀减速直线运动的位移之比为3：2．
根据t=$\frac{v}{a}$知，匀加速和匀减速运动的加速度大小之比为2：3，则匀加速和匀减速运动的时间之比为3：2．
根据平均速度推论知，平均速度均为$\overline{v}=\frac{v}{2}$，则平均速度之比为1：1．
故答案为：3：2，3：2，1：1．
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论，并能灵活运用，也可以先求出平均速度之比，结合时间之比求出位移之比．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
18．加速度是速度的变化量与发生这一变化所用时间的比值，即a=$\frac{△v}{△t}$由此可知（ ）
| A． | A与△v成正比 | B． | A与△v成反比 | ||
| C． | a的方向与△v的方向相反 | D． | a的方向与△v 的方向相同 |
19．
倾角为θ的粗糙斜面上放一质量为m的木块，接触面间的动摩擦因数为μ，现通过一轻质定滑轮沿斜面向上拉木块，拉力的功率恒为P，斜面足够长，则木块可以获得的最大速度为（ ）
倾角为θ的粗糙斜面上放一质量为m的木块，接触面间的动摩擦因数为μ，现通过一轻质定滑轮沿斜面向上拉木块，拉力的功率恒为P，斜面足够长，则木块可以获得的最大速度为（ ）| A． | $\frac{P}{2（mgsinθ+μmgcosθ）}$ | B． | $\frac{2P}{mgsinθ+μmgcosθ}$ | ||
| C． | $\frac{P}{mgsinθ}$ | D． | $\frac{P}{mgsinθ+μmgcosθ}$ |
某导体的伏安特性曲线如图所示，电流是1.5A时，导体的电阻为8Ω，这种导体元件是非线性元件（填“线性”、“非线性”），导体的电阻随导体两端电压的升高而增大．
13．
如图所示，平行板电容器与电动势为E的直流电源连接，上极板A接地．一带负电油滴固定于电容器中的P点．现将平行板电容器的下极板B竖直向下移动一小段距离，则（ ）
如图所示，平行板电容器与电动势为E的直流电源连接，上极板A接地．一带负电油滴固定于电容器中的P点．现将平行板电容器的下极板B竖直向下移动一小段距离，则（ ）| A． | P点的电势将升高 | B． | 电容器的极板带电量将减少 | ||
| C． | 带电油滴所受电场力不变 | D． | 带电油滴的电势能将增大 |
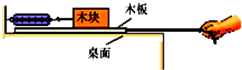如图所示为“研究滑动摩擦力的大小”的实验装置图，将一木块和木板叠放于水平桌面上，弹簧测力计一端固定，另一端与木块水平相连，用力拉动木板，使之在桌面上滑动．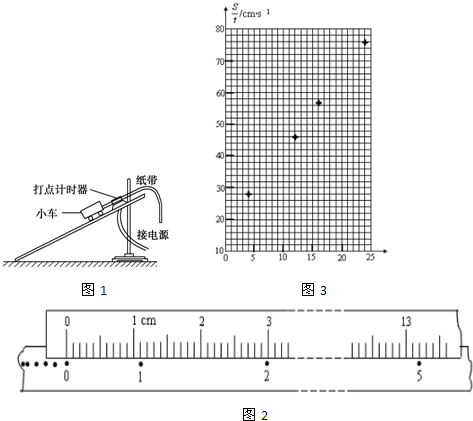
如图所示，是三个阻值不等的电阻的伏安特性曲线，将它们并联接在某电路中时，功率最大的是R1；串联接在某电路中时，电压最大的是R3．