题目内容
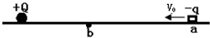 如图所示,绝缘水平面上固定一正点电荷Q,一质量为m、电荷量为-q的小滑块(可看作点电荷)从a点以初速度V0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )
如图所示,绝缘水平面上固定一正点电荷Q,一质量为m、电荷量为-q的小滑块(可看作点电荷)从a点以初速度V0沿水平面向Q运动,到达b点时速度减为零.已知a、b间距离为s,滑块与水平面间的动摩擦因数为μ,重力加速度为g.以下判断正确的是( )A、此过程中产生的热能为
| ||||
B、滑块在运动过程的中间时刻,速度大小等于
| ||||
| C、滑块在运动过程中所受的库仑力一定小于滑动摩擦力 | ||||
D、Q产生的电场中,a、b两点间的电势差为Uab=
|
分析:根据滑块的运动情况可分析滑块受力情况,则可知库仑力与滑动摩擦力的大小关系;由滑块的受力情况可确定加速度的变化情况,即可判断中间时刻的速度;
由动能定理可确定过程中产生的内能与动能变化关系;由动能定理可求得两点间的电势差.
由动能定理可确定过程中产生的内能与动能变化关系;由动能定理可求得两点间的电势差.
解答:解:
A、由动能定理可得:Uq-μmgs=0-
mv02,产生的内能Q=μmgs=Uq+
mv02,因此在此过程中产生的内能大于动能的减少.故A错误;
B、水平方向受大小不变的摩擦力及变大的库仑力,当在滑动过程中,随着间距减小,库仑力增大,但仍小于滑动摩擦力,所以导致加速度慢慢减小,加速度是变化的,故中间时刻的速度不等于
,故B错误;
C、由题意可知,滑块水平方向受库仑力、滑动摩擦力,摩擦力与运动方向相反,而库仑力与运动方相同,因滑块在b点静止,故一定有段时间,库仑力小于滑动摩擦力,当在滑动过程中,随着间距减小,库仑力增大,但仍小于滑动摩擦力,到达b点时速度减为零.故C正确;
D、由动能定理可得:Uabq-μmgs=0-
mv02,解得两点间的电势差为Uab=
,故D正确;
故选:CD.
A、由动能定理可得:Uq-μmgs=0-
| 1 |
| 2 |
| 1 |
| 2 |
B、水平方向受大小不变的摩擦力及变大的库仑力,当在滑动过程中,随着间距减小,库仑力增大,但仍小于滑动摩擦力,所以导致加速度慢慢减小,加速度是变化的,故中间时刻的速度不等于
| v0 |
| 2 |
C、由题意可知,滑块水平方向受库仑力、滑动摩擦力,摩擦力与运动方向相反,而库仑力与运动方相同,因滑块在b点静止,故一定有段时间,库仑力小于滑动摩擦力,当在滑动过程中,随着间距减小,库仑力增大,但仍小于滑动摩擦力,到达b点时速度减为零.故C正确;
D、由动能定理可得:Uabq-μmgs=0-
| 1 |
| 2 |
m(
| ||
| 2q |
故选:CD.
点评:解答本题应注意库仑力随离Q的距离的增大而减小,而滑块的运动可告诉我们最后一定有滑动摩擦力大于库仑力;同时还要明确一定:电场力做功取决于始末位置间的电势差,和路径无关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:
在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求: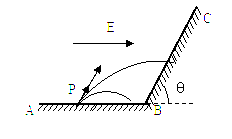
 =1.6m的空间内存在水平向左的匀强电场
=1.6m的空间内存在水平向左的匀强电场 ,质量
,质量 =0.1kg、带电量
=0.1kg、带电量 =+1×
=+1× 的滑块 (视为质点) 以
的滑块 (视为质点) 以 =4m/s的初速度沿水平面向右进入电场区域,滑块与水平面间的动摩擦因数
=4m/s的初速度沿水平面向右进入电场区域,滑块与水平面间的动摩擦因数 =0.4,设最大静摩擦力与滑动摩擦力相等。(g取10m/
=0.4,设最大静摩擦力与滑动摩擦力相等。(g取10m/ )
) 坐标中画出电场力对滑块所做的功
坐标中画出电场力对滑块所做的功 与电场力
与电场力 的关系图象。
的关系图象。
 =1.6m的空间内存在水平向左的匀强电场
=1.6m的空间内存在水平向左的匀强电场 ,质量
,质量 =0.1kg、带电量
=0.1kg、带电量 =+1×
=+1× 的滑块 (视为质点)
以
的滑块 (视为质点)
以 =4m/s的初速度沿水平面向右进入电场区域,滑块与水平面间的动摩擦因数
=4m/s的初速度沿水平面向右进入电场区域,滑块与水平面间的动摩擦因数 =0.4,设最大静摩擦力与滑动摩擦力相等。(g取10m/
=0.4,设最大静摩擦力与滑动摩擦力相等。(g取10m/ )
)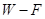 坐标中画出电场力对滑块所做的功
坐标中画出电场力对滑块所做的功 与电场力
与电场力 的关系图象。
的关系图象。