题目内容
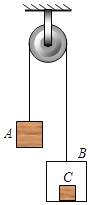
【题目】质量为M的小车A右端固定一根轻弹簧，车静止在光滑水平面上，一质量为m的小物块B从左端以速度v0冲上小车并压缩弹簧，然后又被弹回，回到车左端时刚好与车保持相对静止．求整个过程中弹簧的最大弹性势能EP和B相对于车向右运动过程中系统摩擦生热Q各是多少？
【答案】
，
【解析】
分别研究B从左端运动到弹簧压缩到最短的过程和从初状态到B又回到左端刚好相对静止的过程，由动量和能量关系列出等式求解．
在整个过程中，系统动量守恒，小物块将弹簧压缩到最短和被弹回到车左端的两个时刻，系统的速度是相同的，
设向右为正方向，由动量守恒定律得：mv0=(M+m)v，
由于两个时刻速度相同，说明小物块从车右端返回车左端过程中弹性势能的减小恰好等于系统内能的增加，
即弹簧的最大弹性势能Ep恰好等于返回过程的摩擦生热，而往返两个过程中摩擦生热是相同的，
所以EP是全过程摩擦生热的一半，2Q=EP，
全过程由能量守恒和转过定律得：
联立解得：，
练习册系列答案
相关题目
