题目内容
(12分)质量分别为m1、m2的两木块重叠后放在光滑水平面上,如图所示,m1、m2间的动摩擦因数为μ(认为最大静摩擦力与滑动摩擦力相等),现在m2上施加随时间t增大的力F=kt,式中k是常数。
⑴写出木块m1、m2的加速度a1、a2随时间t变化的关系式;
⑵在给定坐标系内绘出a1、a2随时间t变化的图线,图线上若有转折点,请在坐标轴上标注出该点对应的坐标值。
⑴当0≤t<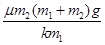 时,a1=a2=
时,a1=a2=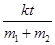 ;当t≥
;当t≥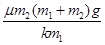 时,a1=
时,a1=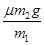 ,a2=
,a2=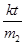 -μg;⑵图略,见解析。
-μg;⑵图略,见解析。
解析试题分析:⑴由于所施加的外力F=kt,因此开始时,F较小,两木块将一起运动,设整体运动的加速度为a,根据牛顿第二定律有:F=(m1+m2)a,所以解得:a1=a2=a=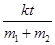
从装置图中可以看出,它们一起运动的最大加速度取决于两者之间的最大摩擦力,有:m1a1<μm2g
联立以上两式解得:t<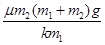
当t≥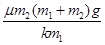 时,对m1,根据牛顿第二定律有:μm2g=m1a1,解得:a1=
时,对m1,根据牛顿第二定律有:μm2g=m1a1,解得:a1=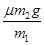
对m2,根据牛顿第二定律有:kt-μm2g=m2a2,解得:a2=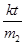 -μg
-μg
即a1、a2随时间t变化的关系式为:当0≤t<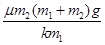 时,a1=a2=
时,a1=a2=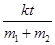
当t≥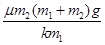 时,a1=
时,a1=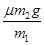 ,a2=
,a2=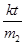 -μg
-μg
所绘a1、a2随时间t变化的关系图线如下图所示。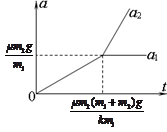
考点:本题主要考查了牛顿第二定律的应用,以及整体法与隔离法的灵活运用问题,属于中档题。

练习册系列答案
相关题目
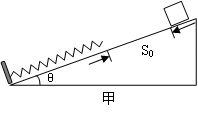
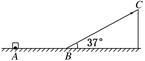
 和滑块到斜面顶端的距离
和滑块到斜面顶端的距离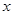 的关系如图2所示。斜面倾角为37°,长为L。有一半径
的关系如图2所示。斜面倾角为37°,长为L。有一半径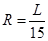 的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知:
的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知: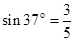 ,
,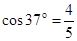 )。求:
)。求: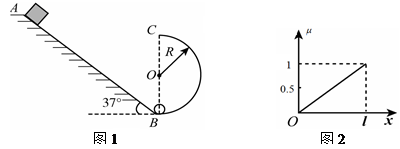
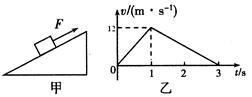
 =1.0m/s的速率逆时针转动。质量为M=1.0kg,长度L2=1.0m的木板上表面与小物块的动摩擦因数μ2=0.4,下表面与水平地面间的动摩擦因数μ3=0.1,开始时长木板靠近传送带B端并处于静止状态。现在传送带上端A无初速地放一个质量为m=1.0kg的小物块,它与传送带之间的动摩擦因数为μ1=0.5,(假设物块在滑离传送带至木板右端时速率不变,sin37o=0.6,cos37 o =0.8, g=10
=1.0m/s的速率逆时针转动。质量为M=1.0kg,长度L2=1.0m的木板上表面与小物块的动摩擦因数μ2=0.4,下表面与水平地面间的动摩擦因数μ3=0.1,开始时长木板靠近传送带B端并处于静止状态。现在传送带上端A无初速地放一个质量为m=1.0kg的小物块,它与传送带之间的动摩擦因数为μ1=0.5,(假设物块在滑离传送带至木板右端时速率不变,sin37o=0.6,cos37 o =0.8, g=10 )。求:
)。求: