题目内容
如图所示,一质量为m=0.5 kg的小滑块,在F=4 N水平拉力的作用下,从水平面上的A处由静止开始运动,滑行x=1.75 m后由B处滑上倾角为37°的光滑斜面,滑上斜面后拉力的大小保持不变,方向变为沿斜面向上,滑动一段时间后撤去拉力。已知小滑块沿斜面上滑到的最远点C距B点为L=2 m,小滑块最后恰好停在A处。不计B处能量损失,g取10 m/s2,已知sin 37°=0.6,cos 37°=0.8。试求: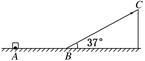
(1)小滑块与水平面间的动摩擦因数μ;
(2)小滑块在斜面上运动时,拉力作用的距离x0;
(3)小滑块在斜面上运动时,拉力作用的时间t。
(1)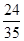 (2)1.25 m(3)0.5 s
(2)1.25 m(3)0.5 s
解析试题分析:(1)小滑块由C运动到A,由动能定理,得
mgsin 37°L-μmgx=0
解得μ=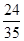
(2)小滑块由A运动到C,由动能定理,得
Fx-μmgx+Fx0-mgsin 37°·L=0
解得x0=1.25 m
(3)小滑块由A运动到B,由动能定理,得
Fx-μmgx=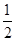 mv2
mv2
由牛顿第二定律,得F-mgsin 37°=ma
由运动学公式,得x0=vt+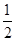 at2
at2
联立解得t=0.5 s
考点:此题考查了动能定理的应用及牛顿第二定律的应用问题.。

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
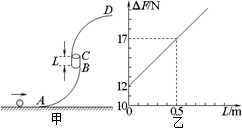
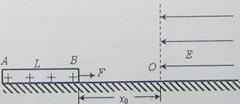

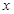 .已知小球质量m,不计空气阻力,求:
.已知小球质量m,不计空气阻力,求: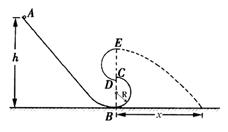
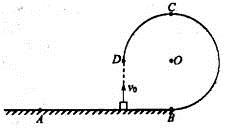
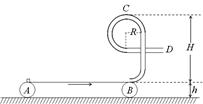
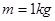 的小物块,从水平面上以速度
的小物块,从水平面上以速度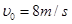 竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数
竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数 =0.4,取
=0.4,取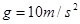 .求:
.求: