题目内容
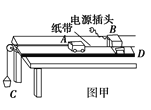
【题目】两位同学分别用如图所示两种装置，通过半径相同的A、B两球的碰撞来做动量守恒定律实验。
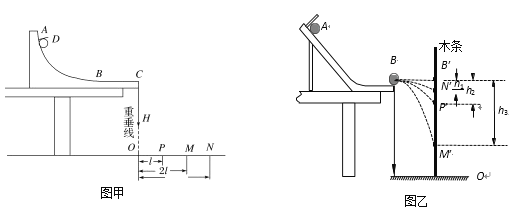
(1)甲同学装置ABC段平整光滑，其中AB段是曲面，BC段是水平面，C端固定一重垂线。O是C的投影点，OC＝H，在轨道上固定一挡板D，从贴紧挡板D处由静止释放小球A，小球A落在M点，用刻度尺测得M点与O点的距离为2l。在C的末端放置小球B，现仍从D处静止释放小球A，小球A与小球B发生正碰，小球B落在N点，小球A落在P点，测得OP为l，若已知小球A与B的质量之比mA：mB=3：1。
①根据实验步骤和上述已知数据，可得ON长度为__________。
②若两小球均看成质点，以两球为系统，通过计算得系统机械能___________（填“守恒”或“不守恒”），可以得出两球的碰撞是____________碰撞。（填“弹性”或“非弹性”）
(2)乙同学改装如图乙所示，将白纸、复写纸固定在竖直放置的木条上，用来记录实验中球A、球B与木条的撞击点。实验时，首先将木条竖直立在轨道末端右侧并与轨道接触，让入射球A从斜轨上起始位置由静止释放，撞击点为B′；然后将木条平移到图中所示位置，入射球A从斜轨上起始位置由静止释放，确定其撞击点为________________；再将入射球A从斜轨上起始位置由静止释放，与球B相撞，确定球A和球B相撞后的撞击点分别为____________和__________。测得B′与N′、P′、M′各点的高度差分别为h1、h2、h3。若所测物理量满足表达式__________________时，则说明球A和球B碰撞中动量守恒。
【答案】
守恒 弹性 
【解析】
(1)①[1]球1运动到C端的速度为
，在空中做平抛运动。水平方向
竖直方向
解得
由于球1两次均从同一高度自由下滑，到C端动能一样，速度均为，设球1与球2碰撞后速度分别为
、
，同理可解得
碰撞前后系统动量守恒，以向右为正方向，以球1和球2为系统，由动量守恒定律得
结合mA：mB=3：1可解得
结合平抛运动的知识可知
②[2][3]以两球为系统，碰前系统初动能
碰后系统末动能
则
，故碰撞过程系统机械能守恒，两球碰撞是弹性碰撞。
(2)[4][5][6]小球做平抛运动，在竖直方向上
解得平抛运动时间
设轨道末端到木条的水平位置为
，则小球做平抛运动的初速度应为
，
，
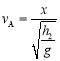故入射球A从斜轨上起始位置由静止释放，确定其撞击点为，碰撞后，确定球A和球B相撞后的撞击点分别为和；
[7]如果碰撞过程动量守恒，则
将
，，
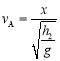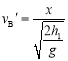
解得
