题目内容
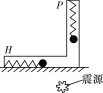
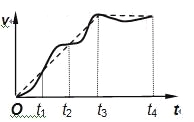
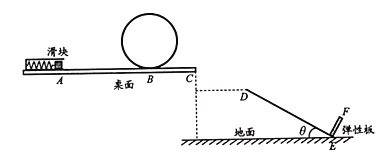
【题目】如图所示是滑块翻越碰撞游戏的示意图。弹射装置将滑块以一定初速度从A点弹出,滑块沿粗糙桌面运动,从B点进入竖直光滑圆轨道,沿圆轨道运动一周后离开轨道,向桌面边缘的C点运动。滑块在C点水平抛出,恰好在D点沿DE方向进入光滑倾斜轨道。固定在轨道底端的弹性板EF与轨道垂直,滑块与弹性板碰撞后反弹,碰撞过程中有能量损失。已知可视为质点的滑块质量m=0.1kg,滑块与桌面间的动摩擦因数μ=0.2,桌面AB和桌面BC长度分别为x1=2.25m与x2=1.0m,CD两点高度差h=0.2m,轨道的倾角θ=30°,DE长度L=0.9m,每次滑块与弹性板碰撞后速度大小变为碰前的0.6倍。
(1)求滑块从C点运动到D的时间;
(2)求滑块在A点的动能大小;
(3)求竖直圆轨道的最大半径;
(4)求滑块在倾斜轨道运动的总距离。
【答案】(1)0.2s(2)1.25J(3)0.32m(4)3.7125m
【解析】
(1)滑块从C到D做平抛运动,则:
h=![]()
代入数据解得
t=0.2s;
(2)设滑块在D的竖直速度为vy,水平速度为vx,滑块在C的速度为vc,则:
vy=gt=2m/s
![]() =tan30°
=tan30°
vc=vx=2![]() m/s
m/s
设滑块在A点的动能为EkA,根据动能定理可得:
![]()
代入数据解得EkA=1.25J;
(3)设滑块在圆弧轨道的最高点速度至少为v,则:
mg=m![]()
设竖直圆轨道的转动半径为R,根据动能定理可得:
![]()
联立解得
R=0.32m
(4)设滑块达到D的速度为vD,则根据运动合成可知:vD=4.0m/s,根据机械能守恒定律可得:
![]()
解得E点的速度
vE=5.0m/s
设第一次碰后的速度为v1、设第二次碰后的速度为v2、设第n次碰后的速度为vn则
v1=3.0m/s
第一次反弹上滑的距离
x1=![]() =0.9m=L
=0.9m=L
第二次反弹上滑的距离
x2=(![]() )2x1=
)2x1=![]() x1,
x1,
第三次反弹上滑的距离
x3=(![]() )2x2=(
)2x2=(![]() )2x1,
)2x1,
第n次反弹上滑的距离
xn=(![]() )2xn-1=(
)2xn-1=(![]() )n-1x1,
)n-1x1,
滑块在倾斜轨道运动的总位移
x=L+2(x1+x2+x3+…+xn)
则
x=0.9m+2×![]() m=3.7125m
m=3.7125m
答:(1)0.2s(2)1.25J(3)0.32m(4)3.7125m

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案