题目内容
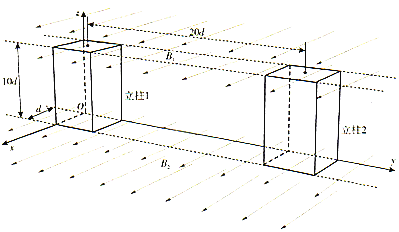
【题目】某研究小组设计了如图所示的双立柱形粒子加速器，整个装置处于真空中。已知两个立柱底面均为边长为d的正方形，各棱均分别和某一坐标轴平行。立柱1下底面中心坐标为
，立柱2下底面中心坐标为
，它们的上底面均位于
的平面内。两个立柱上、下底面间的电压大小均为U，立柱1内存在着沿z轴正方向的匀强电场，立柱2内存在着沿z轴负方向的匀强电场，两立柱外电场均被屏蔽。在
和
的空间内存在着沿x轴正方向的两个匀强磁场，其磁感应强度分别是
和
均未知
。现有大量的带正电的粒子从立柱1底面各处由静止出发，经过立柱1、2加速后能全部回到立柱1的下底面。若粒子在经过
和两个平面时，仅能自由进出两立柱的底面
经过其它位置均会被吸收；该粒子质量为m、电荷量为q，不计粒子重力及粒子间的相互作用力。求：
粒子经过立柱2下底面时的动能
；
磁感应强度和
的大小；
若两立柱上、下底面间电压的大小可调且在粒子运动过程中保持同一定值；两个磁场仅方向可变且保持与z轴垂直。求从立柱1下底面出发的粒子再次回到立柱1下底面的最短时间t。
【答案】（1）2qU；（2）
，
；（3）
【解析】
（1）粒子经过立柱2下底面时，共经过2次加速，根据动能定理：
，
。
（2）要使大量的带正电的粒子从立柱1底面各处由静止出发，经过立柱1、2加速后能全部回到立柱1的下底面，需要立柱1最左面的到达立柱2最左面，立柱1最右面的到达立柱2最右面，第2次加速后亦然，即在磁场中圆周运动半径等于10d。
第一次加速后：
，
，解得
第一次加速后：
，
，解得
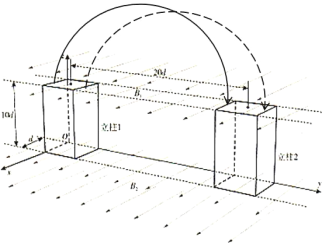
（3）粒子在磁场中的圆周运动时间与粒子速度无关，等于半个周期，所以要减少时间需要减少电场中的运动时间，但是随着速度增加，圆周运动的半径变大，其最大半径为对角线，对应粒子从立柱1最左面的到达立柱2最右面，而且是对角线，如图：
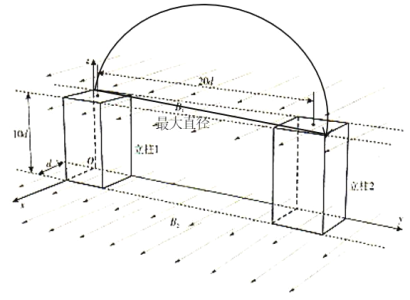
最大半径为
，
由
，
，
解得：
，
；
最短时间为：
，
解得
。
