Question

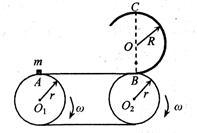
（18分）如图所示，传送带的两个轮子半径均为r=0.2m,两个轮子最高点A、B在同一水平面内，A、B间距离L=5m，半径R=0.4m的固定、竖直光滑圆轨道与传送带相切于B点，C点是圆轨道的最高点．质量m=0.1kg的小滑块与传送带之间的动摩擦因数μ＝0.4，重力加速度g=10m/s²．求：

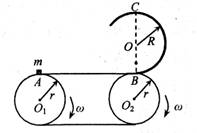
(1)传送带静止不动，小滑块以水平速度v₀滑上传送带，并能够运动到C点，v₀至少多大？

(2)当传送带的轮子以w=10rad/s的角速度转动时，将小滑块无初速地放到传送带上的A点，小滑块从A点运动到B点的时间t是多少？

(3)传送带的轮子以不同的角速度匀速转动，将小滑块无初速地放到传送带上的A点，小滑块运动到C点时，对圆轨道的压力大小不同，最大压力F_m是多大？

 

Answer 1

【答案】

（1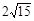）m/s(2) 2.75s(3) 5N

【解析】

试题分析：（1）设小滑块能够运动到C点，在C点的速度至少为v_c，则

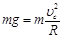 ······························· (2分)

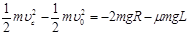  ······················ (2分)

解得v₀=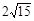m/s  ···························· (1分)

(2)设传送带运动的速度为v₁，小滑块在传送带上滑动时加速度是a，滑动时间是t₁，滑动过程中通过的距离是x，则

v₁=rω...................................... (1分)                 

ma=μmg  ...................(1分)

v₁=at₁...................................... (1分)                

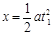......................... (1分)

解得v₁=2m/s，a=4m/s²，t₁=0.5s，x=0.5m

由于x＜L，所以小滑块还将在传送带上与传送带相对静止地向B点运动，设运动时间为t₂，则

L－x= v₁t₂  ······························ (1分)

解得t₂=2.25s

则t= t₁＋t₂=2.75s  ··························· (1分)

（3）轮子转动的角速度越大，即传送带运动的速度越大，小滑块在传送带上加速的时间越长，达到B点的速度越大，到C点时对圆轨道的压力就越大．

小滑块在传送带上一直加速，达到B点的速度最大，设为v_Bm，对应到达C点时的速度为v_cm，圆轨道对小滑块的作用力为F，则

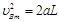  ······························· (2分)

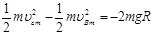  ························ (2分)

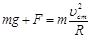  ···························· (1分)

由牛顿第三定律可知对圆轨道的压力F_m=F   ················ (1分)

解得F_m=5N  (1分)

考点：考查力与运动的关系

点评：本题难度较大，本题的难点在于过程过多，对于多过程问题，最好的办法就是大致的对全过程进行运动分析，然后带着问题回到题中，把复杂的多过程拆分为几个小的过程，逐个分析