Question

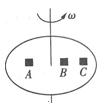
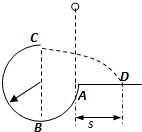
如图所示，竖直平面内的

3

4

圆弧形光滑轨道，轨道半径为R，A端与圆心等高，AD为水平面，B点在圆心的正下方，一小球m自A点正上方由静止释放，自由下落至A点进入轨道，小球巧好能够通过最高点C，求：
（1）小球到B点时的速度v_B；
（2）释放点距A的竖直高度h；
（3）落点D与A的水平距离s．

Answer 1

（1）小球恰好能够通过最高点C，在C点由重力提供向心力 mg=m

v 2C

R

从B到C：-mg2R=

1

2

mv_C²-

1

2

mv_B²
解得：v_B=

5gR

（2）出发点到B由动能定理得：mg（h+R）=

1

2

mv_B²
解得：h=

3

2

R
（3）设小球到达最高点的速度为v_C，从C到D，作平抛运动：s+R=v_Ct
R=

1

2

gt²
由此可解得：s=（

2

-1）R
答：（1）小球到B点时的速度v_B为

5gR

．（2）释放点距A的竖直高度h为

3

2

R；（3）落点D与A的水平距离s为（

2

-1）R．