题目内容
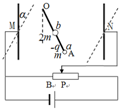 如图,一对很大的竖直放置的平行金属板可以绕M、N左右转动,其之间存在一水平匀强电场.有一长为l的轻质细绝缘棒OA处于电场中,其一端可绕O点在竖直平面内自由转动,另一端A处固定一带电-q、质量为m的小球a,质量为2m的绝缘不带电小球b固定在OA棒中点处.滑动变阻器电阻足够大,当变阻器滑片在P点处时,棒静止在与竖直方向成30°角的位置,已知此时BP段的电阻为R,M、N两点间的距离为d.试求:(重力加速度为g)
如图,一对很大的竖直放置的平行金属板可以绕M、N左右转动,其之间存在一水平匀强电场.有一长为l的轻质细绝缘棒OA处于电场中,其一端可绕O点在竖直平面内自由转动,另一端A处固定一带电-q、质量为m的小球a,质量为2m的绝缘不带电小球b固定在OA棒中点处.滑动变阻器电阻足够大,当变阻器滑片在P点处时,棒静止在与竖直方向成30°角的位置,已知此时BP段的电阻为R,M、N两点间的距离为d.试求:(重力加速度为g)(1)求此时金属板间电场的场强大小E;
(2)若金属板顺时针旋转α=30°(图中虚线表示),并移动滑片位置,欲使棒静止在与竖直方向成30°角的位置,BP段的电阻应调节为多大?
(3)若金属板不转动,将BP段的电阻突然调节为
| 3 |
分析:(1)根据力矩平衡求出金属板间电场的场强大小E;
(2)金属板旋转30°后,电场强度的方向发生改变,板距发生了变化,根据力矩平衡,结合闭合电路欧姆定律求出BP段的电阻的大小.
(3)金属板不转动,将BP段的电阻突然调节为
R,得出电场强度的大小以及电场力的大小,运用动能定理列式求解.
(2)金属板旋转30°后,电场强度的方向发生改变,板距发生了变化,根据力矩平衡,结合闭合电路欧姆定律求出BP段的电阻的大小.
(3)金属板不转动,将BP段的电阻突然调节为
| 3 |
解答:解:(1)小球和棒力矩平衡:2mg
sin30°+mglsin30°=qE1lcos30°
金属板间电场的场强大小E=
(2)金属板间电势差U1=E1d=
金属板旋转30°后平衡,2mg
sin30°+mglsin30°=qE2lsin30°
E=
,板旋转后,板距d′=d cos30°,U2=E′d′=
金属板间电势差与变阻器BP电阻成正比,因此
=
,R2=1.5R
(3)BP段的电阻调节为
R后,E3=
设小球动能最大时,细线与竖直角度为θ,即摆动过程中的平衡位置,根据力矩平衡得到:2mg
sinθ+mglsinθ=qE3lcosθ,tgθ=1,θ=45°.
a的速度是b的2倍,a的质量是b的一半,所以a的动能是 b的动能2倍,设b的最大动能为Ek,对整体,根据动能定理得到:-2mg
(cos30°-cos45°)-mgl(cos30°-cos45°)+qE3l(sin45°-sin30°)=3EK
解得:EK=
≈0.032mgl
答:(1)求此时金属板间电场的场强大小E为
;
(2)BP段的电阻应调节为1.5R;
(3)小球b在摆动过程中的最大动能是0.032mgl.
| l |
| 2 |
金属板间电场的场强大小E=
2
| ||
| 3q |
(2)金属板间电势差U1=E1d=
2
| ||
| 3q |
金属板旋转30°后平衡,2mg
| l |
| 2 |
E=
| 2mg |
| q |
| ||
| q |
金属板间电势差与变阻器BP电阻成正比,因此
| U2 |
| U1 |
| R2 |
| R1 |
(3)BP段的电阻调节为
| 3 |
| 2mg |
| q |
设小球动能最大时,细线与竖直角度为θ,即摆动过程中的平衡位置,根据力矩平衡得到:2mg
| l |
| 2 |
a的速度是b的2倍,a的质量是b的一半,所以a的动能是 b的动能2倍,设b的最大动能为Ek,对整体,根据动能定理得到:-2mg
| l |
| 2 |
解得:EK=
(2
| ||||
| 3 |
答:(1)求此时金属板间电场的场强大小E为
2
| ||
| 3q |
(2)BP段的电阻应调节为1.5R;
(3)小球b在摆动过程中的最大动能是0.032mgl.
点评:本题考查了力矩平衡,动能定理以及闭合电路欧姆定律,综合性较强,对学生能力要求较高,运用动能定理解题时要确定好研究的过程.

练习册系列答案
相关题目

 R,则小球b在摆动过程中的最大动能是多少?
R,则小球b在摆动过程中的最大动能是多少?
 R,则小球b在摆动过程中的最大动能是多少?
R,则小球b在摆动过程中的最大动能是多少?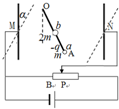 如图,一对很大的竖直放置的平行金属板可以绕M、N左右转动,其之间存在一水平匀强电场.有一长为l的轻质细绝缘棒OA处于电场中,其一端可绕O点在竖直平面内自由转动,另一端A处固定一带电-q、质量为m的小球a,质量为2m的绝缘不带电小球b固定在OA棒中点处.滑动变阻器电阻足够大,当变阻器滑片在P点处时,棒静止在与竖直方向成30°角的位置,已知此时BP段的电阻为R,M、N两点间的距离为d.试求:(重力加速度为g)
如图,一对很大的竖直放置的平行金属板可以绕M、N左右转动,其之间存在一水平匀强电场.有一长为l的轻质细绝缘棒OA处于电场中,其一端可绕O点在竖直平面内自由转动,另一端A处固定一带电-q、质量为m的小球a,质量为2m的绝缘不带电小球b固定在OA棒中点处.滑动变阻器电阻足够大,当变阻器滑片在P点处时,棒静止在与竖直方向成30°角的位置,已知此时BP段的电阻为R,M、N两点间的距离为d.试求:(重力加速度为g) R,则小球b在摆动过程中的最大动能是多少?
R,则小球b在摆动过程中的最大动能是多少?