题目内容
(14分)如图,一对很大的竖直放置的平行金属板可以绕M、N左右转动,其之间存在一水平匀强电场。有一长为l的轻质细绝缘棒OA.处于电场中,其一端可绕O点在竖直平面内自由转动,另一端A.处固定一带电-q、质量为m的小球A.,质量为2m的绝缘不带电小球b固定在OA.棒中点处。滑动变阻器电阻足够大,当变阻器滑片在P点处时,棒静止在与竖直方向成30°角的位置,已知此时BP段的电阻为R,M、N两点间的距离为d。试求:(重力加速度为g)

(1)求此时金属板间电场的场强大小E;
(2)若金属板顺时针旋转α=30°(图中虚线表示),并移动滑片位置,欲使棒静止在与竖直方向成30°角的位置,BP段的电阻应调节为多大?
(3)若金属板不转动,将BP段的电阻突然调节为 R,则小球b在摆动过程中的最大动能是多少?
R,则小球b在摆动过程中的最大动能是多少?
【答案】
(1)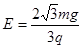 (2)R2=
(2)R2=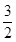 R(3)
R(3)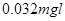
【解析】
试题分析:(1)(4分)小球和棒力矩平衡: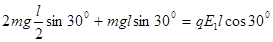
金属板间电场的场强大小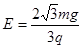
(2)(5分)金属板间电势差U1=E1d=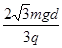
金属板旋转30°后平衡,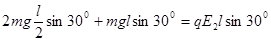
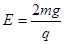 , 板旋转后,板距d′=d cos30°,U2=E′d′=
, 板旋转后,板距d′=d cos30°,U2=E′d′=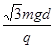
金属板间电势差与变阻器BP电阻成正比,因此 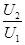 =
=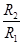 , R2=
, R2=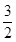 R
R
(3)(5分)BP段的电阻调节为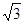 R后,
R后,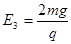
设小球动能最大时,细线与竖直角度为θ,即摆动过程中的平衡位置,根据力矩平衡得到: ,tgθ=1,θ=45°。
,tgθ=1,θ=45°。
A.的速度是b的2倍,A.的质量是b的一半,所以A.的动能是 b的动能2倍,设b的最大动能为Ek,对整体,根据动能定理得到: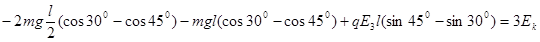
解得: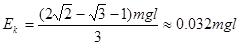
考点:考查了动能定理以及静电学的综合应用
点评:做此类型题目,需要从受力分析开始,因为涉及的过程比较多,所以采用动能定理或者能量守恒分析解题

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目

 R,则小球b在摆动过程中的最大动能是多少?
R,则小球b在摆动过程中的最大动能是多少?