题目内容
1.如图所示,一固定斜面体,其斜边与水平底边的夹角θ=37°,BC为一段光滑圆弧轨道,DE为半圆形光滑轨道,两圆弧轨道均固定于竖直平面内,一滑板静 止在光滑的地面上,右端紧靠C点,上表面所在平面与两圆弧分别相切于C、D两点.一物块被轻放在斜面上F点由静止释放,物块离开斜面后恰好在B点沿切线进入B段 圆弧轨道,再经C点滑上滑板,滑板运动到D点时被牢固粘连.物块可视为质点,质量为m,滑板质量M=2m,DE半圆弧轨道和BC圆弧轨道的半径均为R,斜面体水平底边与滑板上表面的高度差H=2R,板长l=6.5R,板左端到D点的距离L在R<L<5R范围内取值,F点距A点的距离s=12.5R,物块与斜面、物块与滑板间的动摩擦因数均为μ=0.5,重力加速度取g.已知sin37°=0.6,cos37°=0.8.求:(结果用字母 m、g、R、L 表示)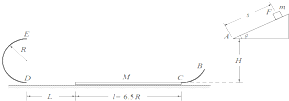
(1)求物块滑到A点的速度大小;
(2)求物块滑到C点时所受圆弧轨道的支持力的大小;
(3)试讨论物块从滑上滑板到离开左端的过程中,克服摩擦力做的功Wf与L的关系; 并判断物块能否滑到DE轨道的中点.
分析 (1)对F到A的过程中,运用动能定理求出物块滑到A点的速度大小.
(2)根据机械能守恒定律求出到达C点的速度,结合牛顿第二定律求出支持力的大小.
(3)根据动量守恒定律求出物块和 滑板达到的共同速度,结合动能定理分别求出物块和滑板的位移大小,判断出物块与滑板达到相同速度时,物块未离开滑板,
讨论当2R≤L<5R和2R≤L<5R,得出滑块的运动规律,结合动能定理分析判断.
解答 解:(1)设物块滑动A点的速度为v1,根据动能定理有:
mgsinθ×12.5R-μmgcosθ×12.5R=$\frac{1}{2}m{{v}_{1}}^{2}$,
解得${v}_{1}=\sqrt{5gR}$.
(2)设物块滑动C点的速度为v2,根据机械能守恒定律有:
$\frac{1}{2}m{{v}_{2}}^{2}=mg2R+\frac{1}{2}m{{v}_{1}}^{2}$,
解得${v}_{2}=3\sqrt{gR}$.
根据牛顿第二定律得,${F}_{N}-mg=m\frac{{{v}_{2}}^{2}}{R}$,
解得${F}_{N}=m\frac{{{v}_{2}}^{2}}{R}+mg=10mg$.
(3)物块从C滑上滑板后开始做匀减速运动,此时滑板开始做匀加速直线运动,当物块与滑板达到共同速度v3时,二者开始做匀速运动.
规定v2的方向为正方向,根据动量守恒定律得,mv2=(m+M)v3,
解得${v}_{3}=\sqrt{gR}$.
对物块根据动能定理有:-μmgl1=$\frac{1}{2}m{{v}_{3}}^{2}-\frac{1}{2}m{{v}_{2}}^{2}$,
对滑板根据动能定理有:$μmg{l}_{2}=\frac{1}{2}M{{v}_{3}}^{2}-0$,
解得l1=8R,l2=2R,
物块相对滑板的位移△l=l2-l1<l,
即物块与滑板达到相同速度时,物块未离开滑板,
讨论:①当R<L<2R,物块在滑板上一直匀减速运动至D,运动的位移为6.5R+L,克服摩擦力做功Wf=μmg(6.5R+L)=$\frac{1}{4}mg(13R+2L)$.
设滑上D点的速度为vD,根据动能定理有:$-μmg(6.5R+L)=\frac{1}{2}m{{v}_{D}}^{2}$-$\frac{1}{2}m{{v}_{2}}^{2}$,
解得$\frac{1}{2}m{{v}_{D}}^{2}=\frac{1}{2}mg(2.5R-L)<mgR$,
所以物块不可能滑到DE轨道的中点.
②当2R≤L<5R,物块先匀减速运动8R,然后匀速运动L-2R,在匀减速运动0.5R,克服摩擦力做功${W}_{f}=μmg(8R+0.5R)=\frac{17}{4}mgR$.
设滑上D点的速度为vD′,根据动能定理有:$-μmg(8R+0.5R)=\frac{1}{2}m{v}_{D}{′}^{2}-\frac{1}{2}m{{v}_{2}}^{2}$,
解得$\frac{1}{2}m{v}_{D}{′}^{2}=\frac{1}{4}mgR<mgR$.
所以 物块不可能滑到DE的中点.
答:(1)物块滑到A点的速度大小为$\sqrt{5gR}$;
(2)物块滑到C点时所受圆弧轨道的支持力的大小为10mg;
(3)当R<L<2R,克服摩擦力做功为$\frac{1}{4}mg(13R+2L)$..不能到达DE的中点.
当2R≤L<5R,克服摩擦力做功为$\frac{17}{4}mgR$.不能到达DE的中点.
点评 本题考查动量守恒和机械能守恒以及有摩擦的板块模型中克服摩擦力做的功.判断物块与滑板在达到相同共同速度时,物块未离开滑板是关键,是一道比较困难的好题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | a、b的速度之差保持不变 | |
| B. | a、b的速度之差与时间成正比 | |
| C. | a、b的速度之和与时间成正比 | |
| D. | a、b的速度之差与时间的平方成正比 |
| A. | 场强的定义式E=$\frac{F}{q}$中,F是放入电场中的电荷所受的力,q是放入电场中的电荷的电量 | |
| B. | 场强的定义式E=$\frac{F}{q}$中,F是放入电场中的电荷所受的力,q是产生电场的电荷的电量 | |
| C. | 在库仑定律的表达式F=$\frac{k{q}_{1}{q}_{2}}{{r}^{2}}$中$\frac{k{q}_{2}}{{r}^{2}}$是电荷q2在q1处产生的场强大小,此场对q1作用的电场力F=q1×k$\frac{{q}_{2}}{{r}^{2}}$,同样k$\frac{{q}_{1}}{{r}^{2}}$是电荷q1产生的电场在点电荷q2处的场强的大小,此场对q2作用的电场力F=q2×k$\frac{{q}_{2}}{{r}^{2}}$ | |
| D. | 无论定义式E=$\frac{F}{q}$中的q值(不为零)如何变化,在电场中的同一点,F与q的比值始终不变 |
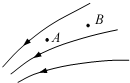
| A. | EA=EB | B. | EA>EB | C. | EA<EB | D. | 无法比较 |
| 位置 | A | B | C | D |
| 时刻t(s) | 0 | 2 | 6 | 8 |
| 速度v(m/s) | 0 | 4 | 4 | 0 |
(2)水平恒力F做的功.
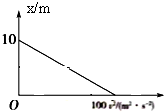 汽车在平直公路上做刹车实验,若从t=0时起汽车在运动过程中的位移x与速度的平方v2之间的关系如图所示,下列说法正确的是( )
汽车在平直公路上做刹车实验,若从t=0时起汽车在运动过程中的位移x与速度的平方v2之间的关系如图所示,下列说法正确的是( )| A. | 刹车过程汽车加速度大小为10m/s2 | B. | 刹车过程持续的时间为5s | ||
| C. | 刹车过程经过3s的位移为7.5m | D. | t=0时汽车的速度为10m/s |
 如图,A、B是电场中一条电场线上的两点,一个正点电荷只受电场力的作用,以初速度v0从A点运动到B点,下列说法正确的是( )
如图,A、B是电场中一条电场线上的两点,一个正点电荷只受电场力的作用,以初速度v0从A点运动到B点,下列说法正确的是( )| A. | 点电荷在B点的加速度一定大于在A点的加速度 | |
| B. | 点电荷在B点的速度一定大于在A点的速度 | |
| C. | 点电荷在B点的电势能一定大于在A点的电势能 | |
| D. | 点电荷在B点受到的电场力一定小于在A点受到的电场力 |
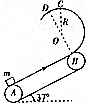 如图所示,传送带与两轮切点A、B间的距离为l=20m,半径为R=0.4m的光滑的半圆轨道与传送带相切于B点,C点为半圆轨道的最高点.BD为半圆轨道直径.物块质量为m=1kg.已知传送带与物块间的动摩擦因数=0.8,传送带与水平面夹角=37°.传送带的速度足够大,已知sin37°=0.6,cos37°=0.8,g=10ms2,物块可视为质点.求:
如图所示,传送带与两轮切点A、B间的距离为l=20m,半径为R=0.4m的光滑的半圆轨道与传送带相切于B点,C点为半圆轨道的最高点.BD为半圆轨道直径.物块质量为m=1kg.已知传送带与物块间的动摩擦因数=0.8,传送带与水平面夹角=37°.传送带的速度足够大,已知sin37°=0.6,cos37°=0.8,g=10ms2,物块可视为质点.求: