题目内容
如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为Ep,现由静止释放A、B,B物块着地后速度立即变为0,同时弹簧锁定解除,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求:
⑴第二次释放A、B后,A上升至弹簧恢复原长时的速度υ1;
⑵第二次释放A、B后,B刚要离地时A的速度υ2.

解:(1)第二次释放A、B后,A、B均做自由落体运动,B着地后,A和弹簧相互作用至A上升到弹簧恢复原长过程中,弹簧对A做的总功为零.(1分)
对A从开始下落到弹簧恢复原长过程中,由机械能守恒定律有: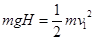 (2分)
(2分)
解得: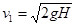 (2分)
(2分)
(2)设弹簧的劲度系数为k,自由长度为L,
第一次释放AB前,设弹簧的形变量为Δx1,有:Δx1=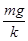 ①(1分),
①(1分),
第一次释放AB后,B刚要离地时弹簧的形变量为Δx2=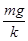 ②(1分)
②(1分)
第二次释放AB后,在B刚要离地时弹簧的形变量为Δx3,则有:Δx3=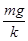 ③(2分)
③(2分)
由①②③得:Δx1=Δx2=Δx3④即这三个状态,弹簧的弹性势能都为Ep(1分)
在第一次释放AB后,对A、B和弹簧组成的系统,从A刚释放到B刚要离地的过程中,由于B的机械能完全转化为内能,故据能量关系有:
mg(H+L-Δx1)+Ep=mg(L+Δx2)+Ep⑤(2分)
在第二次释放AB后,对A、B和弹簧组成的系统,从A刚释放到B刚要离地的过程中,同理由能量关系有:mg(H+L)=mg(L+Δx3)+Ep+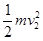 ⑥(4分)
⑥(4分)
由④⑤⑥得: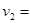
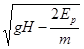 (2分)
(2分)
【解析】略

 (2007?东台市模拟)如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接,只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,将弹簧锁定.现由静止释放A、B,B物块着地时解除弹簧锁定,且B物块的速度立即变为0,在随后的过程中当弹簧恢复到原长时A物块运动的速度为υ0,且B物块恰能离开地面但不继续上升.已知弹簧具有相同形变量时弹性势能也相同.
(2007?东台市模拟)如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接,只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,将弹簧锁定.现由静止释放A、B,B物块着地时解除弹簧锁定,且B物块的速度立即变为0,在随后的过程中当弹簧恢复到原长时A物块运动的速度为υ0,且B物块恰能离开地面但不继续上升.已知弹簧具有相同形变量时弹性势能也相同. (2011?宜昌二模)如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为Ep,现由静止释放A、B,B物块着地后速度立即变为0,同时弹簧锁定解除,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求:
(2011?宜昌二模)如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为Ep,现由静止释放A、B,B物块着地后速度立即变为0,同时弹簧锁定解除,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求: 如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高度,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为Ep,现由静止释放A、B,B物块刚要着地前瞬间将弹簧瞬间解除锁定(解除锁定无机械能损失),B物块着地后速度立即变为0,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求:
如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高度,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为Ep,现由静止释放A、B,B物块刚要着地前瞬间将弹簧瞬间解除锁定(解除锁定无机械能损失),B物块着地后速度立即变为0,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求: