题目内容
 (2007?东台市模拟)如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接,只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,将弹簧锁定.现由静止释放A、B,B物块着地时解除弹簧锁定,且B物块的速度立即变为0,在随后的过程中当弹簧恢复到原长时A物块运动的速度为υ0,且B物块恰能离开地面但不继续上升.已知弹簧具有相同形变量时弹性势能也相同.
(2007?东台市模拟)如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接,只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,将弹簧锁定.现由静止释放A、B,B物块着地时解除弹簧锁定,且B物块的速度立即变为0,在随后的过程中当弹簧恢复到原长时A物块运动的速度为υ0,且B物块恰能离开地面但不继续上升.已知弹簧具有相同形变量时弹性势能也相同.(1)B物块着地后,A向上运动过程中合外力为0时的速度υ1;
(2)B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块运动的位移△x;
(3)第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求第二次释放A、B后,B刚要离地时A的速度υ2.
分析:(1)A到B的过程中,机械能守恒,根据机械能守恒可以求得速度的大小;
(2)B物块恰能离开地面说明此时B与地面之间没有作用力,弹簧的弹力和B的重力大小相等,根据机械能守恒可以求得此时A物块运动的位移△x;
(3)A、B均做自由落体运动,由机械能守恒得刚着地时A、B系统的速度,B物块着地到B刚要离地过程中,弹簧和A物块组成的系统机械能守恒可以求得速度的大小.
(2)B物块恰能离开地面说明此时B与地面之间没有作用力,弹簧的弹力和B的重力大小相等,根据机械能守恒可以求得此时A物块运动的位移△x;
(3)A、B均做自由落体运动,由机械能守恒得刚着地时A、B系统的速度,B物块着地到B刚要离地过程中,弹簧和A物块组成的系统机械能守恒可以求得速度的大小.
解答:解:(1)设A、B下落H过程时速度为υ,由机械能守恒定律有:2mgH=
2mv2
B着地后,A和弹簧相互作用至A上升到合外力为0的过程中,弹簧对A做的总功为零.
即0=
m
-
mv2
解得:v1=

(2)B物块恰能离开地面时,弹簧处于伸长状态,弹力大小等于mg,B物块刚着地解除弹簧锁定时,弹簧处于压缩状态,弹力大小等于mg.因此,两次弹簧形变量相同,则这两次弹簧弹性势能相同,设为EP.
又B物块恰能离开地面但不继续上升,此时A物块速度为0.
从B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块和弹簧组成的系统机械能守恒EP+
m
=mg△x+EP
得△x=H
(3)弹簧形变量x=
△x
第一次从B物块着地到弹簧恢复原长过程中,弹簧和A物块组成的系统机械能守恒EP+
m
=mgx+
m
第二次释放A、B后,A、B均做自由落体运动,由机械能守恒得刚着地时A、B系统的速度为v1=
从B物块着地到B刚要离地过程中,弹簧和A物块组成的系统机械能守恒
m
=mgx+
m
+EP
联立以上各式得v2=
.
答:(1)B物块着地后,A向上运动过程中合外力为0时的速度υ1为
;
(2)B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块运动的位移△x为H;
(3)B刚要离地时A的速度为v2=
.
| 1 |
| 2 |
B着地后,A和弹簧相互作用至A上升到合外力为0的过程中,弹簧对A做的总功为零.
即0=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
解得:v1=
| 2gH |

(2)B物块恰能离开地面时,弹簧处于伸长状态,弹力大小等于mg,B物块刚着地解除弹簧锁定时,弹簧处于压缩状态,弹力大小等于mg.因此,两次弹簧形变量相同,则这两次弹簧弹性势能相同,设为EP.
又B物块恰能离开地面但不继续上升,此时A物块速度为0.
从B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块和弹簧组成的系统机械能守恒EP+
| 1 |
| 2 |
| v | 2 1 |
得△x=H
(3)弹簧形变量x=
| 1 |
| 2 |
第一次从B物块着地到弹簧恢复原长过程中,弹簧和A物块组成的系统机械能守恒EP+
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
第二次释放A、B后,A、B均做自由落体运动,由机械能守恒得刚着地时A、B系统的速度为v1=
| 2gH |
从B物块着地到B刚要离地过程中,弹簧和A物块组成的系统机械能守恒
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
联立以上各式得v2=
2gH-
|
答:(1)B物块着地后,A向上运动过程中合外力为0时的速度υ1为
| 2gH |
(2)B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块运动的位移△x为H;
(3)B刚要离地时A的速度为v2=
2gH-
|
点评:本题的过程比较多,解决本题首先要分析清楚物体的运动的过程,根据不同过程逐个的分析,利用机械能守恒求解即可.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 (2007?东台市模拟)甲、乙两物体同时从同一地点沿同一方向做直线运动的速度-时间图象如图所示,则( )
(2007?东台市模拟)甲、乙两物体同时从同一地点沿同一方向做直线运动的速度-时间图象如图所示,则( ) (2007?东台市模拟)用计算机辅助实验系统(DIS)做验证牛顿第三定律的实验,如图所示是把两个测力探头的挂钩钩在一起,向相反方向拉动,观察显示器屏幕上出现的结果.观察分析两个力传感器的相互作用随着时间变化的曲线,以下结论的不正确的是( )
(2007?东台市模拟)用计算机辅助实验系统(DIS)做验证牛顿第三定律的实验,如图所示是把两个测力探头的挂钩钩在一起,向相反方向拉动,观察显示器屏幕上出现的结果.观察分析两个力传感器的相互作用随着时间变化的曲线,以下结论的不正确的是( ) (2007?东台市模拟)如图,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为Ff.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是( )
(2007?东台市模拟)如图,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为Ff.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是( )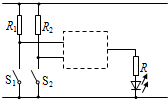 (2007?东台市模拟)如图是一个电工应用某种逻辑电路制作的简单车门报警电路图.图中的两个按钮开关分别装在汽车的两道门上.只要其中任何一个开关处于开路状态,发光二极管就发光.请你根据报警装置的要求,在电路图的虚线框内应是何种电路?( )
(2007?东台市模拟)如图是一个电工应用某种逻辑电路制作的简单车门报警电路图.图中的两个按钮开关分别装在汽车的两道门上.只要其中任何一个开关处于开路状态,发光二极管就发光.请你根据报警装置的要求,在电路图的虚线框内应是何种电路?( )