题目内容
18.一汽车沿平直公路匀加速行驶,经过路旁平行于公路且相距50m的两根相邻电线杆用时5s,它经过第一根电线杆时速度为5m/s,则经过第二根电线杆时的速度为( )| A. | 20m/s | B. | 10m/s | C. | 7.5m/s | D. | 15m/s |
分析 在匀变速直线运动中,物体的平均速度为$\overline{v}=\frac{{v}_{0}+{v}_{t}}{2}=\frac{x}{t}$,据此可正确解答本题.
解答 解:物体经过两根电线杆的平均速度为:$\overline{v}=\frac{x}{t}$=$\frac{50}{5}$=10m/s…①
由于物体做匀加速直线运动,所以有:$\overline{v}=\frac{{v}_{1}+{v}_{2}}{2}$…②
联立①②两式代入数据得:v2=15m/s,即经过第二根电线杆的速度为15m/s,故ABC错误,D正确.
故选:D.
点评 本题考查了运动学推论公式的应用,对于这些推论要会正确推导,明确其适用条件,并能熟练应用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
8.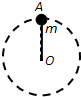 如图所示,长度为0.6m的轻质细杆OA,A端有一质量为3kg的小球,正在以O点为圆心在竖直平面内做圆周运动,已知小球通过最高点时的速度为2m/s,取g=10m/s2.则在小球通过最高点时,轻杆OA将( )
如图所示,长度为0.6m的轻质细杆OA,A端有一质量为3kg的小球,正在以O点为圆心在竖直平面内做圆周运动,已知小球通过最高点时的速度为2m/s,取g=10m/s2.则在小球通过最高点时,轻杆OA将( )
 如图所示,长度为0.6m的轻质细杆OA,A端有一质量为3kg的小球,正在以O点为圆心在竖直平面内做圆周运动,已知小球通过最高点时的速度为2m/s,取g=10m/s2.则在小球通过最高点时,轻杆OA将( )
如图所示,长度为0.6m的轻质细杆OA,A端有一质量为3kg的小球,正在以O点为圆心在竖直平面内做圆周运动,已知小球通过最高点时的速度为2m/s,取g=10m/s2.则在小球通过最高点时,轻杆OA将( )| A. | 受到20N的拉力 | B. | 受到10N的压力 | C. | 受到10N的拉力 | D. | 受到30N的拉力 |
9. 如图甲所示,正方形区域内有垂直于纸面方向的磁场(边界处有磁场),规定磁场方向垂直于纸面向里为正,磁感应强度B随时间t变化的情况如图乙所示.一个质量为m,带电量为+q的粒子,在t=0时刻从O点以速度v0沿x轴正方向射入磁场,粒子重力忽略不计.则下列说法中正确的是( )
如图甲所示,正方形区域内有垂直于纸面方向的磁场(边界处有磁场),规定磁场方向垂直于纸面向里为正,磁感应强度B随时间t变化的情况如图乙所示.一个质量为m,带电量为+q的粒子,在t=0时刻从O点以速度v0沿x轴正方向射入磁场,粒子重力忽略不计.则下列说法中正确的是( )
 如图甲所示,正方形区域内有垂直于纸面方向的磁场(边界处有磁场),规定磁场方向垂直于纸面向里为正,磁感应强度B随时间t变化的情况如图乙所示.一个质量为m,带电量为+q的粒子,在t=0时刻从O点以速度v0沿x轴正方向射入磁场,粒子重力忽略不计.则下列说法中正确的是( )
如图甲所示,正方形区域内有垂直于纸面方向的磁场(边界处有磁场),规定磁场方向垂直于纸面向里为正,磁感应强度B随时间t变化的情况如图乙所示.一个质量为m,带电量为+q的粒子,在t=0时刻从O点以速度v0沿x轴正方向射入磁场,粒子重力忽略不计.则下列说法中正确的是( )| A. | 在T0时刻,若粒子没有射出磁场,则此时粒子的速度方向必沿x轴正方向 | |
| B. | 若B0=$\frac{2πm}{{3q{T_0}}}$,粒子没有射出磁场,T0时刻粒子的坐标为($\frac{3\sqrt{3}{T}_{0}{v}_{0}}{2π}$,$\frac{3{T}_{0}{v}_{0}}{2π}$) | |
| C. | 若粒子恰好没有从y轴射出磁场,则B0=$\frac{5πm}{{3q{T_0}}}$ | |
| D. | 若B0=$\frac{2πm}{{3q{T_0}}}$,粒子没有射出磁场,T0时间内粒子运动的路程为$\frac{{3\sqrt{3}{T_0}{v_0}}}{2π}$ |
6.有一种测量压力的电子秤,其原理图如图1所示.E是内阻不计、电动势为6V的电源.R0是一个阻值为400Ω的限流电阻.G是由理想电流表改装成的指针式测力显示器.R是一个压敏电阻,其阻值可随压力大小变化而改变,其关系如表所示.C是一个用来保护显示器的电容器.秤台的重力忽略不计.
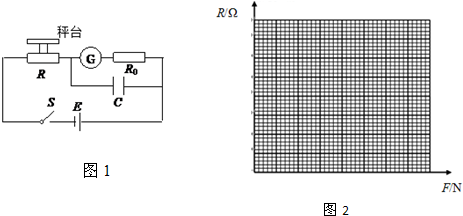
(1)利用表中的数据,以F为横坐标,R为纵坐标,画出所对应的R-F图象;
(2)根据图象写出归电阻R随压力F变化的函数表达式F=1750-$\frac{15}{I}$;
(3)该测力显示器的刻度不是均匀(填是或不是)
(4)若电容器的耐压值为5V,该电子秤的最大称量值为550牛顿.
| 压力F/N | 0 | 50 | 100 | 150 | 200 | 250 | 300 | … |
| 电阻R/Ω | 300 | 280 | 260 | 240 | 220 | 200 | 180 | … |

(1)利用表中的数据,以F为横坐标,R为纵坐标,画出所对应的R-F图象;
(2)根据图象写出归电阻R随压力F变化的函数表达式F=1750-$\frac{15}{I}$;
(3)该测力显示器的刻度不是均匀(填是或不是)
(4)若电容器的耐压值为5V,该电子秤的最大称量值为550牛顿.
3. 图示为伽利略设计的一个斜面实验,让小球沿一个斜面从静止状态开始滚下,小球将滚上另一个斜面,以下说法错误的是( )
图示为伽利略设计的一个斜面实验,让小球沿一个斜面从静止状态开始滚下,小球将滚上另一个斜面,以下说法错误的是( )
 图示为伽利略设计的一个斜面实验,让小球沿一个斜面从静止状态开始滚下,小球将滚上另一个斜面,以下说法错误的是( )
图示为伽利略设计的一个斜面实验,让小球沿一个斜面从静止状态开始滚下,小球将滚上另一个斜面,以下说法错误的是( )| A. | 如果没有摩擦,小球将上升到原来的高度 | |
| B. | 如果没有摩擦,减小后一斜面的倾角,小球仍能到达原来的高度 | |
| C. | 如果没有摩擦,若将后一斜面放平,小球将永远滚动下去 | |
| D. | 因为实验不能做到完全没有摩擦,所以这个实验没有任何意义 |
7.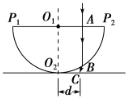 如图所示,半径R=10cm的半圆形玻璃砖放在水平桌面上,O1为圆心,O2为圆弧顶点,P1P2面与桌面平行,现让一很细的激光束垂直P1P2面射入玻璃砖,测得桌面上的亮点C到O2的距离d=4cm,O1A=6cm,则该玻璃砖的折射率为( )
如图所示,半径R=10cm的半圆形玻璃砖放在水平桌面上,O1为圆心,O2为圆弧顶点,P1P2面与桌面平行,现让一很细的激光束垂直P1P2面射入玻璃砖,测得桌面上的亮点C到O2的距离d=4cm,O1A=6cm,则该玻璃砖的折射率为( )
 如图所示,半径R=10cm的半圆形玻璃砖放在水平桌面上,O1为圆心,O2为圆弧顶点,P1P2面与桌面平行,现让一很细的激光束垂直P1P2面射入玻璃砖,测得桌面上的亮点C到O2的距离d=4cm,O1A=6cm,则该玻璃砖的折射率为( )
如图所示,半径R=10cm的半圆形玻璃砖放在水平桌面上,O1为圆心,O2为圆弧顶点,P1P2面与桌面平行,现让一很细的激光束垂直P1P2面射入玻璃砖,测得桌面上的亮点C到O2的距离d=4cm,O1A=6cm,则该玻璃砖的折射率为( )| A. | $\frac{7}{12}$$\sqrt{2}$ | B. | $\frac{7}{6}$$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{5}{3}$ |
10.在距地面高h处,甲球以初速度v0水平抛出,乙球同时以初速度v0沿45°的光滑斜面从高h处开始下滑,若它们同时到达地面,则初速度v0的大小是( )
| A. | $\frac{\sqrt{gh}}{2}$ | B. | $\sqrt{\frac{gh}{2}}$ | C. | $\sqrt{2gh}$ | D. | 2$\sqrt{gh}$ |
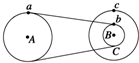 如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,则图中a、b、c各点的线速度之比va:vb:vc=1:1:2.
如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,则图中a、b、c各点的线速度之比va:vb:vc=1:1:2.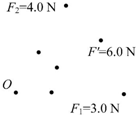 如图所示,是某同学完成验证力的平行四边形定则实验操作后得到的数据图,图中的小圆点分别记录的是O点的位置以及每次细绳的方向.(请你选择合适标度,用力的图示法,作图完成该同学未完成的实验数据处理)
如图所示,是某同学完成验证力的平行四边形定则实验操作后得到的数据图,图中的小圆点分别记录的是O点的位置以及每次细绳的方向.(请你选择合适标度,用力的图示法,作图完成该同学未完成的实验数据处理)