题目内容
 如图所示,滑块质量为m,受一大小为3m
如图所示,滑块质量为m,受一大小为3m| Rg |
| 1 |
| 4 |
分析:根据动能定理可以求出滑块到达C点时的速度,滑块经过C点后做竖直上抛运动,滑块经过P孔又从Q孔落下的过程中,转盘可能刚好转过半个周期,也可能转过整数个周期加半个周期,注意本题的多解性.
解答:解:设滑块至B点时速度为vB,对滑块由A点到B点应用动能定理有:
-μmg5R=
mvB2-
mv02
解得:vB2=8gR
滑块从B点开始运动后机械能守恒,设滑块到达P处时速度为vP,则:
mvB2=
mvP2+mg?2R
解得:vP=2
滑块穿过P孔后再回到平台的时间:
t=
=4
要想实现题述过程,需满足:ωt=(2n+1)π
ω=
(n=0,1,2…)
故平台转动的角速度ω应满足条件为ω=ω=
(n=0,1,2…)
-μmg5R=
| 1 |
| 2 |
| 1 |
| 2 |
解得:vB2=8gR
滑块从B点开始运动后机械能守恒,设滑块到达P处时速度为vP,则:
| 1 |
| 2 |
| 1 |
| 2 |
解得:vP=2
| gR |
滑块穿过P孔后再回到平台的时间:
t=
| 2vp |
| g |
|
要想实现题述过程,需满足:ωt=(2n+1)π
ω=
| π(2n+1) |
| 4 |
|
故平台转动的角速度ω应满足条件为ω=ω=
| π(2n+1) |
| 4 |
|
点评:本题的易错点在于平台转动的角速度的多解性,注意运动的周期性往往带来多解性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011?上海模拟)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
(2011?上海模拟)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3 如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3 (2009?淄博二模)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以
(2009?淄博二模)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以 如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3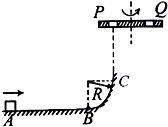 如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3