题目内容
 如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3| gR |
| 1 |
| 4 |
(1)滑块运动到光滑轨道B点时对轨道的压力;
(2)若滑块滑过C点后穿过P孔,求滑块过P点后还能上升的最大高度;
(3)若滑块滑过C点后从P孔上升又恰能从Q孔落下,平台转动的角速度ω应满足什么条件?
分析:(1)对滑块由A点到B点应用动能定理求出B点速度,由牛顿第二定律求出B点时对轨道的压力大小.
(2)对B到P段运用机械能守恒定律求出到达P处的速度,然后由动能定理求出滑块上升的最大高度.
(3)滑块穿过P孔后做竖直上抛运动,根据运动学公式求出竖直上抛的时间,抓住在相等时间内转盘转过的角度等于(2n+1)π,求出平台转动的角速度.
(2)对B到P段运用机械能守恒定律求出到达P处的速度,然后由动能定理求出滑块上升的最大高度.
(3)滑块穿过P孔后做竖直上抛运动,根据运动学公式求出竖直上抛的时间,抓住在相等时间内转盘转过的角度等于(2n+1)π,求出平台转动的角速度.
解答:解:(1)设滑块滑至B点时速度为vB,对滑块由A点到B点过程,
应用动能定理得:-μmg?5R=
mvB2-
mv02,
对滑块在B点,由牛顿第二定律得:N-mg=m
,
解得:N=9mg;
由牛顿第三定律可知,
滑块在B点时对轨道的压力大小N′=N=9mg,方向:向下;
(2)滑块从B点开始运动后机械能守恒,设滑块到达P处时速度为vP,
则
mvB2=
mvP2+mg?2R,解得:vP=2
,
滑块穿过P孔后再上升机械能仍守恒,设能上升的最大高度为h
由
mvP2=mg?h,得到h=2R,
滑块过P点后还能上升的最大高度为2R
(3)滑块穿过P孔后再回到平台的时间
t=
=4
要想实现题述过程,需满足ωt=(2n+1)π
ω=
(n=0、1、2…)
答:(1)滑块运动到光滑轨道B点时对轨道的压力9mg;
(2)若滑块滑过C点后穿过P孔,求滑块过P点后还能上升的最大高度为2R;
(3)若滑块滑过C点后从P孔上升又恰能从Q孔落下,平台转动的角速度ω应满足是:ω=
(n=0、1、2…).
应用动能定理得:-μmg?5R=
| 1 |
| 2 |
| 1 |
| 2 |
对滑块在B点,由牛顿第二定律得:N-mg=m
| VB2 |
| R |
解得:N=9mg;
由牛顿第三定律可知,
滑块在B点时对轨道的压力大小N′=N=9mg,方向:向下;
(2)滑块从B点开始运动后机械能守恒,设滑块到达P处时速度为vP,
则
| 1 |
| 2 |
| 1 |
| 2 |
| gR |
滑块穿过P孔后再上升机械能仍守恒,设能上升的最大高度为h
由
| 1 |
| 2 |
滑块过P点后还能上升的最大高度为2R
(3)滑块穿过P孔后再回到平台的时间
t=
| 2VP |
| g |
|
要想实现题述过程,需满足ωt=(2n+1)π
ω=
| (2n+1)π |
| 4 |
|
答:(1)滑块运动到光滑轨道B点时对轨道的压力9mg;
(2)若滑块滑过C点后穿过P孔,求滑块过P点后还能上升的最大高度为2R;
(3)若滑块滑过C点后从P孔上升又恰能从Q孔落下,平台转动的角速度ω应满足是:ω=
| (2n+1)π |
| 4 |
|
点评:运用动能定理解题首先确定研究对象和研究过程,分析有哪些力做功,根据动能定理列出表达式进行求解.注意在第三问中考虑转动的周期性.

练习册系列答案
相关题目
 (2011?上海模拟)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
(2011?上海模拟)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3 如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3 (2009?淄博二模)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以
(2009?淄博二模)如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以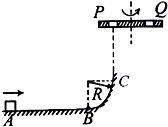 如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3