题目内容
【题目】如图所示,一垂直放置的高为15.0cm的圆柱形中空玻璃容器,其底部玻璃较厚,底部顶点A点到容器底平面中心B点的距离为8.0cm,底部上沿为一凸起的球冠,球心C点在A点正下方,球的半径为1.75cm.已知空气和容器玻璃的折射率分别是n0=1.0和n1=1.56.只考虑近轴光线成像。 已知:当λ《1时,sinλ=λ.
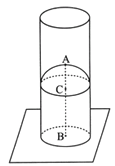
(1)当容器内未装任何液体时,求从B点发出的光线通过平凸玻璃柱,在玻璃柱对称轴上所成的像的位置,并判断像的虚实;
(2)当容器内装满折射率为1.30的液体时,求从B点发出的光线通过平凸玻璃柱的上表面折射后所成像点的位置,并判断这个像的虚实。
【答案】(1) 位置在C点正上方9.75cm处或在B点正上方16.0cm处,实像(2)虚像,在C点正下方26.25cm处或在B点正下方20.0cm处
【解析】
(1)容器底部凸面两侧介质的折射率分别是n1=1.56和n0=1.0。如图,由B点发出的经过球心C的光线BA经过顶点A后,方向不变,进入空气中;由B点发出的与BA成α角的另一条光线BD在D点折射,设折射角为φ,并与前一条出射光线交于E点,E点即B点的像点的位置。

由折射定律和几何关系得
nlsinθ=n0sinφ①
γ=α+θ②
φ=γ+β③
在三角形BCD和三角形CDE中,由正弦定理可得
![]() ④
④
![]() ⑤
⑤
由于只考虑近轴光线成像,所以α、β、θ、φ都是小角度,①④⑤式可写为
n1θ=n0φ ⑥
θ![]() =α
=α![]() ⑦
⑦
φ![]() =β
=β![]() ⑧
⑧
由⑥⑦式可得
α+θ=φ(1+![]() )
)![]() =0.82φ<φ ⑨
=0.82φ<φ ⑨
所考虑的光线是会聚的,故所成的像为实像.由②③⑥⑦⑧式可得
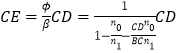
将题给数据代入上式得
![]() 1.75cm=9.75cm ⑩
1.75cm=9.75cm ⑩
由⑨式和题给数据得
![]() =(8.0-1.75+9.75)cm=16.0cm⑩
=(8.0-1.75+9.75)cm=16.0cm⑩
B点发出的光线通过平凸玻璃柱,在玻璃柱对称轴上所成的像点的位置在C点正上方9.75cm处或在B点正上方16.0cm处.
(2)容器底部凸面两侧介质的折射率分别是nl=1.56和n2=1.30.如图,由B点发出的经过球心C的光线BA经过顶点A后,方向不变,进入液体中;由B点发出的与BA成α角的另一条光线BD在D点折射,设折射角为φ,并与前一条出射光线交E点,E点即B点发出的光线第一次折射后所成像点的位置.
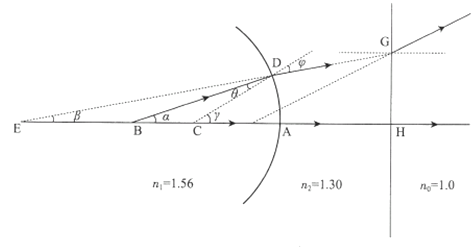
由折射定律和几何关系可得
nlsinθ=n2sinφ(11)
γ=α+θ(12)
γ=φ+β(13)
在三角形BCD和三角形CDE中,由正弦定理可得
![]() (14)
(14)
![]() (15)
(15)
由于只考虑近轴光线成像,所以α、β、θ、φ都是小角度,(11)(14)(15)式可写为
n1θ=n2φ (16)
θ![]() =α
=α![]() (17)
(17)
φ![]() =β
=β![]() (18)
(18)
由(16)(17)式可得
α+θ=φ(1+![]() )
)![]() =1.07φ>φ (19)
=1.07φ>φ (19)
所考虑的光线是发散的,故所成的像为虚像.由(12)(13)(16)(17)(18)式得
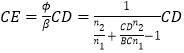
将有关数据代入上式可得:
![]() 1.75cm=26.25cm(20)
1.75cm=26.25cm(20)
由(19)式和题给数据得
![]() =(1.75+26.25-8.0)cm=20.0cm(21)
=(1.75+26.25-8.0)cm=20.0cm(21)
B点发出的光线通过平凸玻璃柱,第一次折射后所成的像点的位置在C点正下方26.25cm处或在B点正下方20.0cm处.