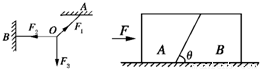
题目内容
如图所示,把长方体分割成A、B两斜面体,质量分别为mA和mB,切面与水平桌面成θ角.两斜面体切面光滑,桌面也光滑.求水平推力在什么范围内,A不会相对B滑动?

 解:A不相对B滑动的临界条件是水平地面对A的支持力为0.
解:A不相对B滑动的临界条件是水平地面对A的支持力为0.以两斜面整体为研究对象有:
F=(mA+mB)a
以物体A为研究对象,其受力如图所示,由牛顿第二定律有,
水平方向:F-F1sinθ=mAa
竖直方向:F1cosθ-mAg=0
联立解得F=

故F的取值范围为0<F≤
 .
.答:水平推力在0<F≤
 范围内,A不会相对B滑动.
范围内,A不会相对B滑动.分析:A不相对B滑动的临界条件是水平地面对A的支持力为0.先以两斜面整体为研究对象根据牛顿第二定律列式,再以物体A为研究对象,对其受力分析,由牛顿第二定律分别列出水平和竖直方向的方程,联立即可求解.
点评:本题主要考查了牛顿第二定律的应用,抓住A不相对B滑动的临界条件是水平地面对A的支持力为0这个突破口,结合整体法和分离法进行求解,难度适中.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目

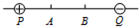 (2012?西城区二模)如图所示,P、Q、A、B四个点在同一条直线上,分别把两个正、负点电荷置于P、Q两点.A、B两点间的电势差用U表示,A点的电场强度用E表示.若只把Q点的点电荷的电荷量减半,则( )
(2012?西城区二模)如图所示,P、Q、A、B四个点在同一条直线上,分别把两个正、负点电荷置于P、Q两点.A、B两点间的电势差用U表示,A点的电场强度用E表示.若只把Q点的点电荷的电荷量减半,则( )