题目内容
16.运动质点沿折线从A到B(位移为x1),B到C(位移为x2),C到D(位移为x3)运动,求出合位移x,并由此总结出求多个矢量的合矢量的一般方法.
分析 矢量合成遵守平行四边形定则或三角形定则,根据合位移与分位移的关系,分析规律,总结方法.
解答 解:由(1)、(2)两图对比可知,A到C的位移等于A到B的位移和B到C位移的合位移,从起点A到终点C.由(2)、(3)对比知,A到D的位移等于A到C的位移和C到D位移的合位移,则$\overrightarrow{x}$=$\overrightarrow{{x}_{1}}$+$\overrightarrow{{x}_{2}}$+$\overrightarrow{{x}_{3}}$
可以看出,求多个矢量的合矢量的方法是:两个矢量合成后再与第三个矢量合成,依次将各个矢量逐个合成,就能得到合矢量.
答:合位移$\overrightarrow{x}$=$\overrightarrow{{x}_{1}}$+$\overrightarrow{{x}_{2}}$+$\overrightarrow{{x}_{3}}$.求多个矢量的合矢量的方法是:两个矢量合成后再与第三个矢量合成,依次将各个矢量逐个合成,就能得到合矢量.
点评 解决本题的关键要掌握矢量合成的方法,明确分位移与合位移的关系.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
6.多用电表调零后,用“×10”挡测量一个电阻的阻值,发现表针偏转角度极小,正确的判断和做法是( )
| A. | 这个电阻值很小 | |
| B. | 这个电阻值很大 | |
| C. | 为了把电阻测得更准一些,应换用“×1”挡,重新调零后再测量 | |
| D. | 为了把电阻测得更准一些,应换用“×100”挡,重新调零后再测量 |
7.一辆汽车从车站匀加速直线开出,初速度为零.开出一段时间之后,司机发现一乘客未上车,便紧急刹车做匀减速运动.从启动到停止一共经历t=10s,前进了16m,在此过程中,汽车的最大速度为( )
| A. | 1.6m/s | B. | 3.2m/s | C. | 3m/s | D. | 无法确定 |
4. 内壁光滑的绝缘材料制成圆轨道固定在倾角为θ的斜面上,与斜面的交点是A,直径AB垂直于斜面,直径CD和MN分别在水平和竖直方向上.它们处在水平方向的匀强电场中.质量为m、电荷量为q的小球(可视为点电荷)刚好能静止于圆轨道内的A点.现对在A点的该点电荷施加一沿圆环切线方向的瞬时冲量,使其恰能绕圆环完成圆周运动.下列对该点电荷运动的分析,正确的是( )
内壁光滑的绝缘材料制成圆轨道固定在倾角为θ的斜面上,与斜面的交点是A,直径AB垂直于斜面,直径CD和MN分别在水平和竖直方向上.它们处在水平方向的匀强电场中.质量为m、电荷量为q的小球(可视为点电荷)刚好能静止于圆轨道内的A点.现对在A点的该点电荷施加一沿圆环切线方向的瞬时冲量,使其恰能绕圆环完成圆周运动.下列对该点电荷运动的分析,正确的是( )
 内壁光滑的绝缘材料制成圆轨道固定在倾角为θ的斜面上,与斜面的交点是A,直径AB垂直于斜面,直径CD和MN分别在水平和竖直方向上.它们处在水平方向的匀强电场中.质量为m、电荷量为q的小球(可视为点电荷)刚好能静止于圆轨道内的A点.现对在A点的该点电荷施加一沿圆环切线方向的瞬时冲量,使其恰能绕圆环完成圆周运动.下列对该点电荷运动的分析,正确的是( )
内壁光滑的绝缘材料制成圆轨道固定在倾角为θ的斜面上,与斜面的交点是A,直径AB垂直于斜面,直径CD和MN分别在水平和竖直方向上.它们处在水平方向的匀强电场中.质量为m、电荷量为q的小球(可视为点电荷)刚好能静止于圆轨道内的A点.现对在A点的该点电荷施加一沿圆环切线方向的瞬时冲量,使其恰能绕圆环完成圆周运动.下列对该点电荷运动的分析,正确的是( )| A. | 小球一定带负电 | B. | 小球运动到B点时动能最小 | ||
| C. | 小球运动到M点时动能最小 | D. | 小球运动到D点时机械能最小 |
11. 内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量为m的小球甲,另一端固定有质量为2m的小球乙,将两小球放入凹槽内,小球乙位于凹槽的最低点,如图所示.由静止释放后( )
内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量为m的小球甲,另一端固定有质量为2m的小球乙,将两小球放入凹槽内,小球乙位于凹槽的最低点,如图所示.由静止释放后( )
 内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量为m的小球甲,另一端固定有质量为2m的小球乙,将两小球放入凹槽内,小球乙位于凹槽的最低点,如图所示.由静止释放后( )
内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为$\sqrt{2}$R的轻杆,一端固定有质量为m的小球甲,另一端固定有质量为2m的小球乙,将两小球放入凹槽内,小球乙位于凹槽的最低点,如图所示.由静止释放后( )| A. | 下滑过程中甲球减少的机械能总小于乙球增加的机械能 | |
| B. | 下滑过程中甲球减少的重力势能总等于乙球增加的重力势能 | |
| C. | 甲球可沿凹槽下滑到槽的最低点 | |
| D. | 杆从右向左滑回时,乙球一定能回到凹槽的最低点 |
2.在距地面高为h处,同时以大小相等的初速度分别平抛,竖直上抛,竖直下抛质量相等的物体(空气阻力不计),它们从抛出到落地的过程中动量的增量( )
| A. | 三者一样大 | B. | 平抛过程最大 | ||
| C. | 竖直下抛过程最大 | D. | 竖直上抛过程最大 |
9.关于万有引力定律,下列说法中正确的是( )
| A. | 万有引力定律是卡文迪许利用扭秤实验发现的 | |
| B. | 万有引力定律是牛顿在总结前人研究的基础上发现的 | |
| C. | 万有引力定律只是严格适用于两个质点之间 | |
| D. | 公式F=$\frac{G{m}_{1}{m}_{2}}{{r}^{2}}$中的r是指两个质点间的距离或两个均匀球体的球心间的距离 |
6.矩形金属线圈在匀强磁场中匀速转动.产生的感应电流与时间关系如图所示.下列说法正确的是( )
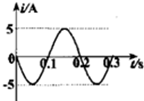

| A. | 交变电流的有效值为5$\sqrt{2}$A | B. | t=0.1s时线圈磁通量为零 | ||
| C. | 交变电流的频率为50Hz | D. | 交变电流的周期为0.2s |
7.在下图的图象中,是匀变速直线运动的图象是( )
| A. | 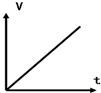 | B. | 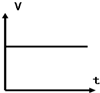 | C. |  | D. |  |