Question

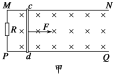
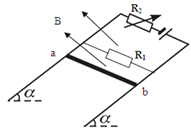
【题目】在倾角α=37°的斜面上，固定着间距L=1m的平行金属导轨，其电阻不计,导轨接入如图所示的电路中，已知电源的电动势E=30V、内阻r=1.0Ω，可变电阻R2大小可调，定值电阻R1=6Ω．一根质量m=1.0kg的金属棒ab垂直导轨放置，其电阻Rab=3Ω,整个装置放在磁感应强度B=10T、垂直于斜面向上的匀强磁场中。已知ab棒与导轨间的动摩擦因数μ＝0.5，sin37°=0.6，cos37°=0.8，g取10m/s2，假设金属棒的最大静摩擦力等于滑动摩擦力．问要使金属棒静止在导轨上R2最小值为多少？

Answer 1

【答案】17Ω

【解析】

试题分析：根据导体棒刚要发生滑动时，金属棒受到中的电流最大，对应此时的电阻最小，结合欧姆定律，共点力平衡条件分析解题

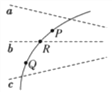
若金属棒静止在导轨上，R2调到最小时，金属棒受到沿斜面向下的摩擦力且为最大静摩擦力， ab棒受力如图所示：

由平衡条件得：F=mgsin37°+μmgcos37° ①

安培力为：F=BIabL ②

由①②式联立解得：Iab=1A ③

Rab和R1并联电阻为： ④

设电路中的总电流为I，则I R并=IabRab ⑤

由闭合电路欧姆定律得： ⑥

由③④⑤⑥得：R2=17Ω

所以R2最小可调到17Ω