题目内容
4.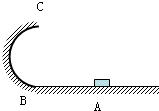 如图所示,半圆形竖直光滑轨道BC与水平轨道AB相连接,一滑块在恒定外力作用下,以a=$\frac{5}{2}$g的加速度从水平轨道上的A点由静止出发,到B点时撤去外力.已知滑块质量为m,圆形轨道半径为R,A、B间距为2R.求:滑块通过最高点C时对轨道压力的大小.
如图所示,半圆形竖直光滑轨道BC与水平轨道AB相连接,一滑块在恒定外力作用下,以a=$\frac{5}{2}$g的加速度从水平轨道上的A点由静止出发,到B点时撤去外力.已知滑块质量为m,圆形轨道半径为R,A、B间距为2R.求:滑块通过最高点C时对轨道压力的大小.
分析 在AB段由运动学公式求的到达B点的速度,在从B到C的过程中,由动能定理求得C点的速度,根据牛顿第二定律求的作用力
解答 解:到达B点的速度为v,从A到B的过程中,由速度位移公式可得2as=v2
解得$v=\sqrt{10gR}$
从B到C由动能定理可得$-mg•2R=\frac{1}{2}{mv}_{C}^{2}-\frac{1}{2}m{v}^{2}$
在C点由牛顿第二定律可得$mg+{F}_{N}=\frac{{mv}_{C}^{2}}{R}$
联立解得FN=5mg
答:滑块通过最高点C时对轨道压力的大小为5mg
点评 本题注意应分段分析,不同的过程采用不同的物理规律求解,特别要注意在竖直面上的圆周运动中利用牛顿第二定律即可

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.飞机在高空水平匀速飞行,某时刻自由释放a球,1s后又自由释放b球,不计空气阻力,两球在落地前( )
| A. | a球在b球的前下方 | |
| B. | a球在b球的后下方 | |
| C. | a球始终在b球的正下方5m处 | |
| D. | a球始终在b球的正下方,但两者之间的距离逐渐变大 |
12. 如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )
如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )
 如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )
如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )| A. | $\frac{{r}_{1}{ω}_{1}}{{r}_{3}}$ | B. | $\frac{{r}_{3}{ω}_{3}}{{r}_{1}}$ | C. | $\frac{{r}_{3}{ω}_{1}}{{r}_{2}}$ | D. | $\frac{{r}_{1}{ω}_{1}}{{r}_{2}}$ |
19.关于机械能是否守恒的叙述,正确的是( )
| A. | 作匀速直线运动的物体机械能一定守恒 | |
| B. | 作匀变速直线运动的物体机械能一定守恒 | |
| C. | 合外力对物体做功为零时,机械能一定守恒 | |
| D. | 只有重力对物体做功,物体机械能一定守恒 |
9. 6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )
6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )
 6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )
6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )| A. | 与地球具有相同的公转周期 | |
| B. | 公转线速度比地球的小 | |
| C. | 向心加速度比地球的小 | |
| D. | 设L2点到太阳的距离为R1,地球到太阳的距离为R2,周期分别为T1、T2,则$\frac{{R}_{1}^{3}}{{T}_{1}^{2}}$=$\frac{{R}_{2}^{3}}{{T}_{2}^{2}}$ |
16.地球的同步卫星是指相对于地面静止不动的人造卫星( )
| A. | 它可以在地面上任一点的正上方,且离地心距离可按需要选择不同的值 | |
| B. | 它可以在地面上任一点的正上方,但离地心距离是一定的 | |
| C. | 它只能在赤道的正上方,但离地心的距离可按需要选择不同的值 | |
| D. | 它只能在赤道的正上方,且离地心的距离是一定的 |
13.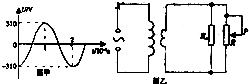 理想变压器原、副线圈的匝数比为5:1.原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器R的滑动片.下列说法正确的是( )
理想变压器原、副线圈的匝数比为5:1.原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器R的滑动片.下列说法正确的是( )
 理想变压器原、副线圈的匝数比为5:1.原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器R的滑动片.下列说法正确的是( )
理想变压器原、副线圈的匝数比为5:1.原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器R的滑动片.下列说法正确的是( )| A. | 副线圈输出电压的频率为100Hz | |
| B. | 副线圈输出电压的有效值为62V | |
| C. | P向上移动时,原、副线圈的电流都减小 | |
| D. | P向上移动时,变压器的输出功率增加 |
14.无线电技术的发展给人类带来了极大的便利,以下有关电磁波的说法,正确的是( )
| A. | 电磁波不能在真空中传播 | |
| B. | 电磁波具有反射、干涉、衍射和偏振等现象,但不会发生折射 | |
| C. | 在通讯中广泛应用的无线电波是电磁波谱中波长最短的 | |
| D. | 手机使用过程中发射的无线电波都是经过调制的 |
 小郑同学想在家里做用单摆测定重力加速度的实验,但没有合适的摆球,他找到了一块大小约为3cm,外形不规则的大理石块代替小球.他设计的实验步骤是:
小郑同学想在家里做用单摆测定重力加速度的实验,但没有合适的摆球,他找到了一块大小约为3cm,外形不规则的大理石块代替小球.他设计的实验步骤是: