题目内容
(1)如图所示,根据玻尔理论,①、②、③是氢原子发生的三种可能的跃迁,与它们对应的光谱线分别记为Ⅰ、Ⅱ、Ⅲ.则下列光谱图中,与上述光谱正确对应的是哪个图?(图下方标的数值表示以纳米为单位的波长)

(2)如图所示,EF为水平地面,0点左侧是粗糙的,右侧是光滑的,一轻质弹簧右端固定在墙壁上,左端与静止在0点、质量为m的小物块A连接,弹簧处于原长状态.一质量为2m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动,已知物块B与地面EO段间的滑动摩擦力大小为
 ,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F.物块B和物块A可视为质点.已知CO=5L,OD=L.求:
,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F.物块B和物块A可视为质点.已知CO=5L,OD=L.求: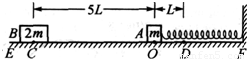
①撤去外力后弹簧的最大弹性势能?
②从D点返回后,物块B从O点开始向左运动直到静止所用的时间是多少?
【答案】分析:(1)根据能级差算出三种光子的能量,然后根据能量与波长关系,求出三种光的波长即可正确解答.
(2)①根据动能定理求出B物体运动到O时的速度,碰撞过程由于内力远远大于外力,动量守恒,根据动量守恒求出碰后AB共同速度,然后根据功能关系求解.
②根据功能关系求出AB一起返回到O点时的速度,此后A与B将分离,对B根据动量定理可求出其停止所用时间.
解答:解:(1)由能级变化关系可知①②③种情况下向外放出的光子能量;波长、波速、频率相关计算得频率值,光子能量计算可知BCD错误,A正确.
故选A.
(2)设B与A碰撞前速度为v,由动能定理得:

解得:
B与A在0点碰撞,设碰后共同速度为v1,由动量守恒得:
2mv=(2m+m)v1
解得:
碰后B和A一起运动,当它们的共同速度减小为零时,弹簧的弹性势能最大,设为Epm,则由能量守恒得:

解得:
故撤去外力后弹簧的最大弹性势能为: .
.
(2)设A、B一起回到0点的速度为v2.由机械能守恒有:

所以:
经过0点后,B和A分离,B在滑动摩擦力的作用下做匀减速度直线运动,设运动时间为t1,由动量定理得:

解得:
故从D点返回后,物块B从O点开始向左运动直到静止所用的时间是: .
.
点评:本题难点在于(2)题,考查了动量守恒与功能关系的综合应用,注意把复杂的过程分解为多个小过程,同时A与B碰撞过程中有能量损失,这点也是很多学生容易忽视的.
(2)①根据动能定理求出B物体运动到O时的速度,碰撞过程由于内力远远大于外力,动量守恒,根据动量守恒求出碰后AB共同速度,然后根据功能关系求解.
②根据功能关系求出AB一起返回到O点时的速度,此后A与B将分离,对B根据动量定理可求出其停止所用时间.
解答:解:(1)由能级变化关系可知①②③种情况下向外放出的光子能量;波长、波速、频率相关计算得频率值,光子能量计算可知BCD错误,A正确.
故选A.
(2)设B与A碰撞前速度为v,由动能定理得:

解得:

B与A在0点碰撞,设碰后共同速度为v1,由动量守恒得:
2mv=(2m+m)v1
解得:

碰后B和A一起运动,当它们的共同速度减小为零时,弹簧的弹性势能最大,设为Epm,则由能量守恒得:

解得:

故撤去外力后弹簧的最大弹性势能为:
 .
.(2)设A、B一起回到0点的速度为v2.由机械能守恒有:

所以:

经过0点后,B和A分离,B在滑动摩擦力的作用下做匀减速度直线运动,设运动时间为t1,由动量定理得:

解得:

故从D点返回后,物块B从O点开始向左运动直到静止所用的时间是:
 .
.点评:本题难点在于(2)题,考查了动量守恒与功能关系的综合应用,注意把复杂的过程分解为多个小过程,同时A与B碰撞过程中有能量损失,这点也是很多学生容易忽视的.

练习册系列答案
相关题目
 如图1所示,在用斜槽轨道做“研究平抛物体运动”的实验中,
如图1所示,在用斜槽轨道做“研究平抛物体运动”的实验中,




