题目内容
2.计算一个天体的质量,需要知道绕着该天体做匀速圆周运动的另一星球的条件是( )| A. | 质量和运转周期 | B. | 运转周期和轨道半径 | ||
| C. | 运转速度 | D. | 运转速度和质量 |
分析 根据万有引力提供向心力,只要知道轨道半径与线速度、或周期、或角速度,即可求出中心天体的质量.
解答 解:根据GMmr2=mr4π2T2GMmr2=mr4π2T2得,M=4π2r3GT24π2r3GT2,只要知道另一星球运转的周期和轨道半径,即可求出该天体的质量,故A错误,B正确.
根据GMmr2=mv2rGMmr2=mv2r得,M=v2rGv2rG,只要知道另一星球的线速度和轨道半径,即可求出该天体的质量,故C、D错误.
故选:B.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,知道运用该理论,只能求出中心天体的质量.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
12.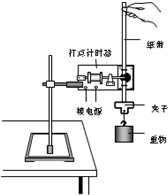 利用如图所示的装置可以研究自由落体运动.实验中需要调整好仪器,接通打点计时器的电源,松开纸带,使重物下落.打点计时器会在纸带上打出一系列的小点.为了测得重物下落的速度和加速度,还需要的实验器材有( )
利用如图所示的装置可以研究自由落体运动.实验中需要调整好仪器,接通打点计时器的电源,松开纸带,使重物下落.打点计时器会在纸带上打出一系列的小点.为了测得重物下落的速度和加速度,还需要的实验器材有( )
 利用如图所示的装置可以研究自由落体运动.实验中需要调整好仪器,接通打点计时器的电源,松开纸带,使重物下落.打点计时器会在纸带上打出一系列的小点.为了测得重物下落的速度和加速度,还需要的实验器材有( )
利用如图所示的装置可以研究自由落体运动.实验中需要调整好仪器,接通打点计时器的电源,松开纸带,使重物下落.打点计时器会在纸带上打出一系列的小点.为了测得重物下落的速度和加速度,还需要的实验器材有( )| A. | 天平 | B. | 秒表 | C. | 毫米刻度尺 | D. | 弹簧测力计 |
13.物体的加速度有两个表达式a=△v△t△v△t和a=FmFm,关于这两个表达式,下面说法不正确的是( )
| A. | a与△v成正比,与△t成反比 | |
| B. | a与F成正比,与m 成反比 | |
| C. | 前一式表示a是描述速度变化的快慢,后式表明a由F与m决定的 | |
| D. | 两式均为矢量式,前一式中a与△v方向相同,后一式中a与F方向相同 |
10.下列关于功的叙述中,正确的是( )
| A. | 力和位移是做功的二要素,只要有力、有位移、就一定有功 | |
| B. | 功等于力、位移、力与位移夹角的正弦三者的乘积 | |
| C. | 因为功是矢量,所以功有正负 | |
| D. | 一对作用力和反作用力所做的功代数和可以不为零 |
17.两个质点之间万有引力的大小为F,如果将这两个质点之间的距离变为原来的3倍,那么它们之间万有引力的大小变为( )
| A. | F3F3 | B. | 9F | C. | F9F9 | D. | F27F27 |
14.甲物体的质量是乙物体质量的3倍,它们从同一点由静止同时开始下落,不计空气阻力,则下列说法正确的是( )
| A. | 甲比乙先着地 | |
| B. | 甲比乙加速度大 | |
| C. | 甲与乙着地速度不相同 | |
| D. | 下落过程中,两者在任意时刻离地的高度相同 |
11.一个物体从静止出发以加速度a做匀加速直线运动.经过时间t后,改作以t时刻末的速度做匀速直线运动,则在2t时间内的平均速度是( )
| A. | 3434at | B. | 4343at | C. | 1212at |
6.将闭合多匝线圈置于仅随时间变化的磁场中,线圈平面与磁场方向垂直,关于线圈中产生的感应电动势和感应电流,下列表述正确的是( )
| A. | 穿过线圈的磁通越大,感应电动势越大 | |
| B. | 穿过线圈的磁通量变化越大,感应电动势越大 | |
| C. | 穿过线圈的磁通量变化越快,感应电动势越大 | |
| D. | 感应电流产生的磁场方向与原磁场方向始终相同 |
 如图所示,质量为1kg的物体在离斜面底端O点4m的A点由静止滑下,若动摩擦因数均为0.5,斜面倾角为37°,斜面与平面间由一小段圆弧连接,取g=10m/s2,求:
如图所示,质量为1kg的物体在离斜面底端O点4m的A点由静止滑下,若动摩擦因数均为0.5,斜面倾角为37°,斜面与平面间由一小段圆弧连接,取g=10m/s2,求: