Question

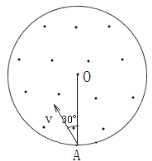
【题目】如图有一半径为R的弹性圆形边界，内有垂直于纸面向外的磁感应强度为B的磁场，现有一比荷为的带正电的粒子由A点与OA成30°角垂直入射到磁场中，之后粒子与边界发生弹性碰撞（垂直于边界的速度碰后反向，大小不变，平行边界的速度不变），在粒子绕边界一周的过程中，有（ ）

A.粒子每相邻两次碰撞的时间间隔为

B.粒子每次与边界相碰时的速度与过该碰撞点的切线的夹角均为60°

C.当时，粒子仍能回到A点

D.当时，粒子仍能回到A点

Answer 1

【答案】BCD

【解析】

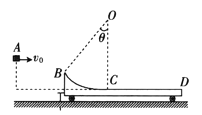
A．粒子在圆形磁场中做匀速圆周运动，第一次从A到B的轨迹如图所示：

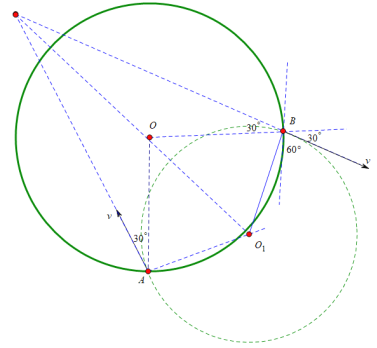
因不知道运动的半径，故无法确定圆心角，运动时间无法求出，故A错误；

B．进入磁场时与半径OA成30°角，由运动的对称性可知，出射方向与半径OB成30°角，则粒子与边界相碰时的速度与过该碰撞点的切线的夹角均为60°，故B正确；

C．若，可知运动的半径为

可知圆心角为120°，相对的圆形磁场所夹角为120°，根据运动的对称性和周期性可知，圆形磁场的360°分成3个120°，则经过三个圆弧运动刚好回到A点，故C正确；

D．若，可知运动的半径为

可知圆心角为180°，相对的圆形磁场所夹角为60°，根据运动的对称性和周期性可知，的360°分成6个60°，则经过六个圆弧运动刚好回到A点，故D正确。

故选BCD。