��Ŀ����
����Ŀ����ͼ��ʾ���뾶ΪR�İ�Բ�������ڷֲ��Ŵ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB����Բ����ߴ�ֱx�����һ���ӷ���װ�ã��ڣ�R��y��R�������ڸ�������x��������ͬʱ�����һ�����������ӣ�����������Ϊm���������Ϊq�����ٶȾ�Ϊv�����������Ӽ������þ����Բ��ƣ��������Ӷ��ܵ���y�ᣬ�������y������ӱ����ȵ���y�����������tʱ�䣬��(����)

A. ���ӵ���y���λ��һ��������ͬ
B. �ų�����뾶RӦ���� ![]()
C. ![]() �����нǶ����Ļ���ֵ����
�����нǶ����Ļ���ֵ���� ![]()
D. ![]()
���𰸡�C
��������A����������ų���������Բ���˶������˶��켣��ͼ��ʾ��
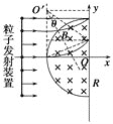
y=��R������ֱ����ֱ���������˶�����y�ᣬ���������ڴų��з���ƫת����ͼ��֪������ƫת������Ҳ�п��ܴ���y=R��λ���ϣ�������Щ���ӿ��ܻᵽ��y���ͬһλ�ã���A����
B����x���غ���������ӣ����켣�뾶���ڴų��뾶��������ǡ�ô�y����R����������켣�뾶С��R�������Ӳ��ܴ�y�������������Ӵ�y������������ǹ켣�뾶r��R����![]() ����B����
����B����
CD�������ڴų����˶�ʱ���ʱ���켣��Ӧ�ҳ��������x���غϷ������䣬�켣��Ӧ���ҳ���켣Բ�Ľ�Ϊ�����ɼ��ι�ϵ��![]() �������˶�ʱ��Ϊ
�������˶�ʱ��Ϊ![]() ����y����R����������˶�ʱ����̣�
����y����R����������˶�ʱ����̣�![]() ����ʱ���Ϊ
����ʱ���Ϊ![]() ����C��ȷ��D������
����C��ȷ��D������
��ѡC��