题目内容
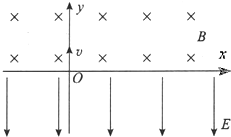如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B．在x轴下方有沿y轴负方向的匀强电场，场强为E，一质量为m，电荷量为-q的粒子从坐标原点O沿着y轴正方向射出，射出之后，第二次到达x轴时，它与点O的距离为L，不计粒子所受重力．求（1）此粒子射出的速度v．
（2）粒子从坐标原点O射出之后，第二次到达x轴时运动的总路程及时间．
分析：粒子在磁场中做圆周运动，转动半周后到达电场先减速再反向加速，以大小不变的速度反向进入磁场，再次偏转；由题意可知半径大小，由洛仑兹力充当向心力可求得粒子的速度；粒子的总路程包括电场中的路程和磁场中的路程，总时间等于做圆周运动的时间和做匀变速时间之和．
解答：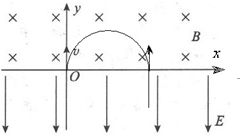
解：由题意知第2次经过x轴的运动如图所示
由几何关系：圆周运动半径 r=
洛伦兹力提供圆周运动向心力
Bqv=m
解得：v=
电场中做匀变速直线运动，设粒子进入电场作减速运动的最大路程为l，加速度为a，则有：
v2=2al
a=
解得l=
运动的总路程 s=πr+2l=
+
粒子做圆周运动的时间t1=
T=
，
粒子做匀减速运动的时间t2=
=
所以粒子在电场中运动的时间t3=2t2=
则运动的总时间为：t=t1+t3=
+
答：（1）此粒子射出的速度为
．
（2）粒子从坐标原点O射出之后，第二次到达x轴时运动的总路程为
+
，时间为
+
．
解：由题意知第2次经过x轴的运动如图所示由几何关系：圆周运动半径 r=
| L |
| 2 |
洛伦兹力提供圆周运动向心力
Bqv=m
| v2 |
| r |
解得：v=
| qBL |
| 2m |
电场中做匀变速直线运动，设粒子进入电场作减速运动的最大路程为l，加速度为a，则有：
v2=2al
a=
| qE |
| m |
解得l=
| qB2L2 |
| 8mE |
运动的总路程 s=πr+2l=
| πL |
| 2 |
| qB2L2 |
| 4mE |
粒子做圆周运动的时间t1=
| 1 |
| 2 |
| πm |
| Bq |
粒子做匀减速运动的时间t2=
| v |
| a |
| BL |
| 2E |
所以粒子在电场中运动的时间t3=2t2=
| BL |
| E |
则运动的总时间为：t=t1+t3=
| πm |
| Bq |
| BL |
| E |
答：（1）此粒子射出的速度为
| qBL |
| 2m |
（2）粒子从坐标原点O射出之后，第二次到达x轴时运动的总路程为
| πL |
| 2 |
| qB2L2 |
| 4mE |
| πm |
| Bq |
| BL |
| E |
点评：带电粒子在磁场中的题目关键在于明确圆心和半径，注意要根据题意找出合理的运动过程，从而得出正确的结论．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在x轴上方有匀强磁场B，一个质量为m，带电量为-q的粒子，以速度v从O点射入磁场，θ角已知，粒子重力不计，粒子在磁场中的运动时间为（ ）
如图所示，在x轴上方有磁感应强度为B、方向垂直纸面向里的均匀磁场，x轴下方有电场为E、方向竖直向下的均匀电场，现有一质量为m、电量为q的粒子从y轴上某一点由静止开始释放，重力忽略不计，为使它能到达x轴上位置为x=L的一点Q，求：
如图所示，在x轴上方存在垂直于纸面向里的匀强磁场，磁场的磁感应强度为B．在xOy平面内，从原点O处沿与x轴正方向成θ角（0＜θ＜π）以速率v发射一个带正电的粒子（重力不计）．则下列说法正确的是（ ）
如图所示，在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场．一个不计重力的带电粒子从坐标原点O处以速度v进入磁场，粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角，若粒子从x轴上的P点射出磁场，已知p点与O点的距离为a，则该粒子的比荷和所带电荷的正负是（ ）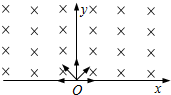
如图所示，在x轴上方（y≥0）存在着垂直于纸面向里的匀强磁场，磁感强度为B．在原点O有一离子源向x轴上方的各个方向发射出质量为m、电量为q的正离子，速率都为υ，对那些在xOy平面内运动的离子，在磁场中到达的最大x坐标和最大y坐标各是多少？