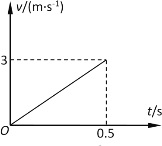
题目内容
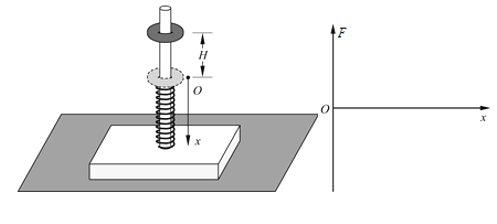
【题目】如图所示,一光滑杆固定在底座上,构成支架,放置在水平地面上,光滑杆沿竖直方向,一轻弹簧套在光滑杆上。一圆环套在杆上,圆环从距弹簧上端H处由静止释放,接触弹簧后,将弹簧压缩,弹簧的形变始终在弹性限度内。已知圆环的质量为m,支架的质量为3m,弹簧的劲度系数为k,重力加速度为g,不计空气阻力。取圆环刚接触弹簧时的位置为坐标原点O,竖直向下为正方向,建立x轴。
(1)在圆环压缩弹簧的过程中,圆环所受合力为F,请在图中画出F随x变化的示意图;
(2)借助F-x图像可以确定合力做功的规律,在此基础上,求圆环在下落过程中最大速度vm的大小。
(3)试论证当圆环运动到最低点时,底座对地面的压力FN > 5mg。
【答案】(1)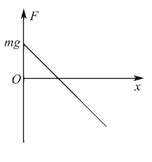 (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据受力及弹力的变化可知:在圆环压缩弹簧的过程中,F随x变化的示意图如图所示
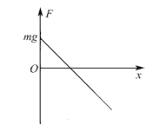
(2)在运动过程中当合力为零时,圆环的速度有最大值,设圆环速度最大时弹簧的形变量为x,根据牛顿第二定律有:![]()
在此过程中,根据F- x图线与x轴围成的面积可求得圆环所受合力做的功:![]()
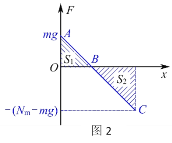
从圆环开始下落到圆环速度达到最大的过程中,
根据动能定理有:![]()
所以:![]()
(3)当圆环运动到最低点时圆环速度为零,弹簧的弹力最大(设为Nm),底座对地面的压力FN最大。
设从平衡位置到最低点的过程中,圆环所受合力做的功为W2。
根据动能定理,从接触弹簧到平衡位置的过程中有:![]()
从平衡位置到最低点的过程中有:![]()
根据公式可知:![]() , 即
, 即![]()
结合图像可知,![]() ,即
,即![]()
设地面对底座的支持力大小为F。取底座为研究对象,根据牛顿第二定律有:![]()
所以:![]()
根据牛顿第三定律,底座对地面的压力大小![]() ,所以:
,所以:![]()

练习册系列答案
相关题目