��Ŀ����
����Ŀ����ͼ��ʾ����ֱ������ϵ0��x��L����������y�����������ǿ�糡���ڱ߳�Ϊ2L��������abcd�������߽磩���з���ֱֽ���������ǿ�ų���һ���Ӵ�y���ϵ�A��0�� ![]() �����Դ�СΪv0���ٶ���x������������糡����֪���ӵ�����Ϊm�������Ϊe��������abcd����������Ϊ��3L��0������ab����x��ƽ�У���ǿ�糡�ĵ糡ǿ�ȴ�С
�����Դ�СΪv0���ٶ���x������������糡����֪���ӵ�����Ϊm�������Ϊe��������abcd����������Ϊ��3L��0������ab����x��ƽ�У���ǿ�糡�ĵ糡ǿ�ȴ�С![]() ��
��
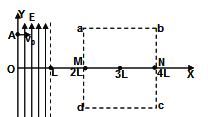
��1������ӽ���ų�ʱ��λ�����ꣻ
��2����Ҫʹ�����ڴų��д�ab�����������ǿ�ų��ĴŸ�Ӧǿ�ȴ�СB�����������
���𰸡���1����2L��0����2��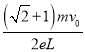 ��B��
��B��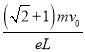
����������������������ڵ糡������ƽ���˶����ֱ��г���ֱ��ˮƽ����ķ��̣�����������ӽ���ų�ʱ��λ�����ꣻ���Ӵ�ab�߽���������˶��켣���ٽ�״̬�ֱ���ab���к�bc���У����ݼ��ι�ϵ�����Ӧ�뾶�������������ṩ�������������ǿ�ų��ĴŸ�Ӧǿ�ȴ�СB�����������
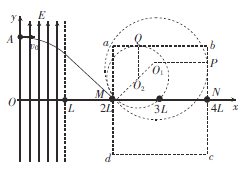
��1�������ڵ糡������ƽ���˶����켣��ͼ��ʾ�����У�
��ֱ�����У� ![]()
���ٶ�Ϊ�� ![]()
ˮƽ������Ϊ�� ![]()
��ֱ�ٶȣ�vy��at1
��ã�y1��![]() vy��v0
vy��v0
���Ե�������糡ʱ���ٶȷ�����x���45���ǣ�������ڵ糡����x�����������y�Ḻ�����˶��ľ���ֱ�ΪL��![]() ������ΪA��������ǣ�0��
������ΪA��������ǣ�0�� ![]() �����������糡�ʹų���������������ֱ���˶������������ų�����λ������Ϊ��2L��0��������ų������ٶȴ�С��v��
�����������糡�ʹų���������������ֱ���˶������������ų�����λ������Ϊ��2L��0��������ų������ٶȴ�С��v��![]() v0��������x���45���ǡ�
v0��������x���45���ǡ�
��2����ʹ���Ӵ�ab�߽���������˶��켣���ٽ�״̬�ֱ���ab���к�bc����
���˶��켣��ab����ʱ����r1��r1sin45����L
�����ڴų����˶��������������ṩ���������У� ![]()
��ã� 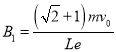
���˶��켣��bc����ʱ���У�r2��r2sin45����2L
�����ڴų����˶��������������ṩ���������У� ![]()
��ã� 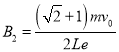
��ǿ�ų��ĴŸ�Ӧǿ�ȴ�СB����������� 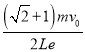 ��B��
��B��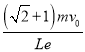

 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�