题目内容
如图所示，长为2m的小车A，它的质量为2kg，静止在光滑的水平地面上，一个质量为3kg、大小可忽略的物体B从车A的左端以4m/s的水平向右的速度冲上小车A，物体B在车A上滑行了0.8m后，它们相对静止。之后，小车A跟右边的墙壁发生碰撞，碰撞时间极短，且碰撞过程中无能量损失，g=10m/s2，求：（1）碰壁前，两物相对静止时，小车A的动能多大。（2）为保证两物相对静止之后，车才与墙壁碰撞，开始时，车的右端距墙至少多远。（3）车与墙第一次碰撞后离墙最远时，A、B系统的机械能。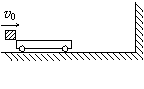
（17分）解：（1）设碰壁前两物相对静止时，小车A的速度为v1，以A、B为研究对象，根据动量守恒定律得：mBv0=(mA+mB)v1 （3分）∴v1=2.4m/s EkA=
mAv12=5.76J （2分）（2）设从开始相互作用到相对静止，A、B两物体的位移分别为sA、sB，根据动能定理得：μmBgsA=mA
（3分） -μmBgsB=mB-mB
（3分） sB-sA=0.8m （1分）∴sA=0.48m 故开始时，车的右端距墙至少为0.48m （1分）（3）车与墙碰后，车以原速率反向运动，当车速为零时离墙最远，设此时B的速度为v2A与B组成的系统根据动量守恒定律得：mBv1-mAv1=mBv2 （2分） ∴v2=0.8m/s∴此时A与B组成的系统的机械能为：E=EkB=mBv22=0.96J （2分）
mAv12=5.76J （2分）（2）设从开始相互作用到相对静止，A、B两物体的位移分别为sA、sB，根据动能定理得：μmBgsA=mA （3分） -μmBgsB=mB-mB （3分） sB-sA=0.8m （1分）∴sA=0.48m 故开始时，车的右端距墙至少为0.48m （1分）（3）车与墙碰后，车以原速率反向运动，当车速为零时离墙最远，设此时B的速度为v2A与B组成的系统根据动量守恒定律得：mBv1-mAv1=mBv2 （2分） ∴v2=0.8m/s∴此时A与B组成的系统的机械能为：E=EkB=mBv22=0.96J （2分） 
练习册系列答案
相关题目
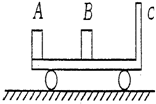如图所示，长为2L的板面光滑且不导电的平板小车C放在光滑水平面上，车的右端有档板，车的质量mC=4m．今在静止的平板车的左端放一个带电量为+q．质量为m的物块A，在中间位置放一个绝缘物体B，质量为mB=2m．在整个空间加上一个水平方向的匀强电场时，金属块A由静止开始向右运动，并以速度v0与B发生碰撞，碰后A以
