题目内容
如图所示，在直角坐标系xOy的原点O处有一放射源S，放射源S在xOy平面内均匀发射速度大小相等的正电粒子，位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN，荧光屏正反两侧均涂有荧光粉，MN与x轴交于O'点。已知三角形MNO为正三角形，放射源S射出的粒子质量为m，带电荷量为q，速度大小为v，不计粒子的重力。
（1）若只在y轴右侧加一平行于x轴的匀强电场，要使y轴右侧射出的所有粒子都能打到荧光屏MN上，试求电场强度的最小值Emin及此条件下打到荧光屏M点的粒子的动能；
（2）若在xOy平面内只加一方向垂直纸面向里的匀强磁场，要使粒子能打到荧光屏MN的反面O'点，试求磁场的磁感应强度的最大值Bmax；
（3）若在xOy平面内只加一方向垂直纸面向里的匀强磁场，磁感应强度与（2）题中所求Bmax相同，试求粒子打在荧光屏MN的正面O'点所需的时间t1和打在荧光屏MN的反面O'点所需的时间t2之比。
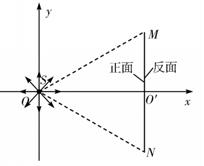
解析：（1）所加电场电场强度的最小值Emin对应沿着y轴正方向射出的带电粒子正好打在荧光屏的端点M这一临界状态。对该粒子有：
，
， （4分）
解得
（1分）
对此时从S射出能打到荧光屏上的任一粒子（包括打到荧光屏M点的粒子），设它到达屏时的动能为Ek，由动能定理有：
（2分）
解得：
（1分）
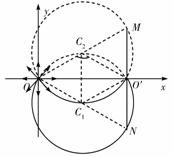
（2）由题意，所加磁场的最大磁感应强度Bmax对应来自S的粒子恰好经过荧光屏下端点N后打到O’这一临界状态，如图所示(圆心在C1)。从图中的几何关系得，粒子在磁场中做圆周运动的半径
（2分）
洛伦兹力提供向心力，有
，（2分）联立解得
（2分）
（3）打在荧光屏正面O点的粒子的圆弧轨迹见图(圆心在C2)，根据匀速圆周运动规律有
，
，由图中的几何关系得
，联立解得t1:t2=1∶2 （4分）
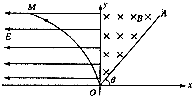如图所示，在直角坐标平面的第I象限内有一匀强磁场区域，磁感应强度为B，直线OA是磁场右侧的边界．在第Ⅱ象限区域，存在电场强度大小为E的水平向左的匀强电场，y轴是电场、磁场区域的分界线曲线，OM满足方程x=-ky2（k＞0）．有一带电荷量为q、质量为m的负粒子（重力不计）在曲线OM上某一点由静止释放，穿越y轴进入磁场中．
（2013?怀化二模）如图所示，在直角坐标xOy平面y轴左侧（含y轴）有一沿y轴负向的匀强电场，一质量为m，电量为q的带正电粒子从x轴上P处以速度ν0沿x轴正向进入电场，从y轴上Q点离开电场时速度变为2ν0，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的矩形匀强磁场区域（图中未画出，粒子过Q点继续运动一段距离后才进入磁场区域），磁场磁感应强度大小
如图所示，在直角坐标xOy平面y轴左侧（含y轴）有一沿y轴负向的匀强电场，一质量为m，电量为q的带正电粒子从x轴上P处以速度v0沿x轴正向进入电场，从y轴上Q点离开电场时速度方向与y轴负向夹角θ=30°，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的有界匀强磁场区域（图中未画出），磁场磁感应强度大小B=
如图所示，在直角坐标xoy的第一象限中分布着指向－y轴方向的匀强电场，在第四象限中分布着垂直纸面向里方向的匀强磁场，一个质量为m、带电＋q的粒子(不计重力)在A点(0，3)以初速V0＝120m/s平行x轴射入电场区域，然后从电场区域进入磁场，又从磁场进入电场，并且只通过x轴上的P点(6，0)和Q点(8，0)各一次，已知该粒子的荷质比为q/m＝108c/kg．
沿x轴正向进入电场，从y轴上Q点离开电场时速度方向与y轴负向夹角
，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的有界匀强磁场区域（图中未画出），磁场磁感应强度大小
，粒子能从坐标原点O沿x轴负向再进入电场．不计粒子重力，求：