题目内容
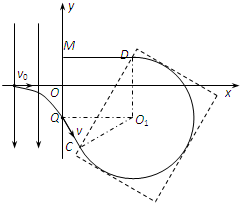
 (2013?怀化二模)如图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度ν0沿x轴正向进入电场,从y轴上Q点离开电场时速度变为2ν0,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的矩形匀强磁场区域(图中未画出,粒子过Q点继续运动一段距离后才进入磁场区域),磁场磁感应强度大小B=
(2013?怀化二模)如图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度ν0沿x轴正向进入电场,从y轴上Q点离开电场时速度变为2ν0,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的矩形匀强磁场区域(图中未画出,粒子过Q点继续运动一段距离后才进入磁场区域),磁场磁感应强度大小B=| mv0 | qd |
(1)求粒子进入磁场时速度方向与y轴负向的夹角θ和电场强度E的大小;
(2)绘出粒子P-M运动的轨迹图,求粒子进入磁场至M点的运动时间;
(3)求矩形匀强磁场区域的最小面积.
分析:(1)由粒子进入磁场速度为2v0,由几何关系可得角度关系.带电粒子进入匀强电场后,受重力和电场力,由动能定理可得电场强度
(2)进入磁场后在洛伦兹力作用下做圆周运动,由左手定则可以判定受力,进而确定其转动方向,作图可得运动轨迹,由运动轨迹的几何关系可得圆心角,进而得到圆周运动的时间,DM段粒子做匀速运动可得此段的时间,相加得总时间.
(3)由运动轨迹图,可以找出磁场边长的最小值,可得最小面积.
(2)进入磁场后在洛伦兹力作用下做圆周运动,由左手定则可以判定受力,进而确定其转动方向,作图可得运动轨迹,由运动轨迹的几何关系可得圆心角,进而得到圆周运动的时间,DM段粒子做匀速运动可得此段的时间,相加得总时间.
(3)由运动轨迹图,可以找出磁场边长的最小值,可得最小面积.
解答:(1)设粒子从Q点离开电场时速度大小为v,
由粒子在匀强电场中做类平抛运动,故其水平速度不变,由几何关系得:sinθ=
=
,解得:θ=30°
由动能定理得:qEd=
mν2-
m
解得:E=
(2)设粒子从C点进入、D点离开矩形匀强磁场区域.
粒子在磁场中做匀速圆周运动半径为r,圆心为O1,如图所示.
由洛伦兹力提供向心力,得:qvB=
解得 r=
=2d
设粒子在磁场中做匀速圆周运动时间为t1,D到M时间为t2
由图中的几何关系可得圆周运动的圆心就为:
圆周运动的周期为:T=
=
故圆周运动时间为:t1=
=
DM段为匀速运动故时间为:t2=
=
粒子从进入磁场到M的总时间:t=t1+t2=
(3)若矩形磁场区域的面积最小,则如图虚线区域:
可得长边:L1=2r=4d
短边:L2=r+rsinθ=3d
磁场区域的最小面积:S=L1L2=12d2
答:
(1)粒子进入磁场时速度方向与y轴负向的夹角θ=30°,电场强度E的大小E=
;
(2)绘出粒子P-M运动的轨迹图,求粒子进入磁场至M点的运动时间t=
;
(3)求矩形匀强磁场区域的最小面积S=12d2.
由粒子在匀强电场中做类平抛运动,故其水平速度不变,由几何关系得:sinθ=
| v0 |
| 2v0 |
| 1 |
| 2 |
由动能定理得:qEd=
| 1 |
| 2 |
| 1 |
| 2 |
| ν | 2 0 |
解得:E=
3m
| ||
| 2qd |
(2)设粒子从C点进入、D点离开矩形匀强磁场区域.
粒子在磁场中做匀速圆周运动半径为r,圆心为O1,如图所示.

由洛伦兹力提供向心力,得:qvB=
| mv2 |
| r |
| mv |
| qB |
设粒子在磁场中做匀速圆周运动时间为t1,D到M时间为t2
由图中的几何关系可得圆周运动的圆心就为:
| 4π |
| 3 |
圆周运动的周期为:T=
| 2πr |
| 2v0 |
| πr |
| v0 |
故圆周运动时间为:t1=
| 4πr |
| 3v |
| 4πd |
| 3ν0 |
DM段为匀速运动故时间为:t2=
| DM |
| 2ν0 |
2
| ||
| 3ν0 |
粒子从进入磁场到M的总时间:t=t1+t2=
(4π+2
| ||
| 3v0 |
(3)若矩形磁场区域的面积最小,则如图虚线区域:
可得长边:L1=2r=4d
短边:L2=r+rsinθ=3d
磁场区域的最小面积:S=L1L2=12d2
答:
(1)粒子进入磁场时速度方向与y轴负向的夹角θ=30°,电场强度E的大小E=
3m
| ||
| 2qd |
(2)绘出粒子P-M运动的轨迹图,求粒子进入磁场至M点的运动时间t=
(4π+2
| ||
| 3v0 |
(3)求矩形匀强磁场区域的最小面积S=12d2.
点评:本题考查了带电粒子在匀强电场中的类平抛运动,在磁场中的匀速圆周运动,对数学的几何能力要求较高,关键画出粒子的轨迹图,结合牛顿第二定律以及向心力等知识进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?怀化二模)如图所示,在坐标系xOy中,有边长为a的正方形均匀铜线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行,下边界足够远.t=0时刻,线圈以恒定的速度V(平动)沿垂直于磁场上边界的方向穿过磁场区域.则在线圈穿越磁场区域的过程中,ab间的电势差Uab随时间t变化的图线是下图中的( )
(2013?怀化二模)如图所示,在坐标系xOy中,有边长为a的正方形均匀铜线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行,下边界足够远.t=0时刻,线圈以恒定的速度V(平动)沿垂直于磁场上边界的方向穿过磁场区域.则在线圈穿越磁场区域的过程中,ab间的电势差Uab随时间t变化的图线是下图中的( ) (2013?怀化二模)如图,将一个负电荷在除电场力外的力作用下从电场线上的a点移到b点,重力忽略不计,a、b两点间距离为d,电势?a=10V、?b=5V.下列判断正确的是( )
(2013?怀化二模)如图,将一个负电荷在除电场力外的力作用下从电场线上的a点移到b点,重力忽略不计,a、b两点间距离为d,电势?a=10V、?b=5V.下列判断正确的是( ) (2013?怀化二模)如图所示是质量为1kg的滑块在水平面上做直线运动的υ-t图象.下列判断正确的是( )
(2013?怀化二模)如图所示是质量为1kg的滑块在水平面上做直线运动的υ-t图象.下列判断正确的是( ) (2013?怀化二模)如图,在粗糙的水平面上,静置一矩木块,木块由A、B两部分组成,A的质量是B的6倍,两部分接触面竖直且光滑,夹角θ=30°,现用一与侧面垂直的水平力F推着B木块贴着A匀速运动,A木块依然保持静止,则A受到的摩擦力大小与水平力F大小之比为(
(2013?怀化二模)如图,在粗糙的水平面上,静置一矩木块,木块由A、B两部分组成,A的质量是B的6倍,两部分接触面竖直且光滑,夹角θ=30°,现用一与侧面垂直的水平力F推着B木块贴着A匀速运动,A木块依然保持静止,则A受到的摩擦力大小与水平力F大小之比为( (2013?怀化二模)如图为一折射率为
(2013?怀化二模)如图为一折射率为