题目内容
4. 甲、乙、丙三球的质量分别为2m,m,m排成的一直线放在光滑水平面上,如图所示,乙球与丙球靠在一起,且为静止,甲球以速度v向它们运动,若他们在对心碰撞中无机械能损失,求三球最终的速度?
甲、乙、丙三球的质量分别为2m,m,m排成的一直线放在光滑水平面上,如图所示,乙球与丙球靠在一起,且为静止,甲球以速度v向它们运动,若他们在对心碰撞中无机械能损失,求三球最终的速度?
分析 碰撞过程系统动量守恒,碰撞过程不损失机械能,应用动量守恒定律与机械能守恒定律分析答题.
解答 解:由于甲球与球乙发生碰撞时间极短,乙球的位置来不及发生变化,
这样乙球对球丙也就无法产生力的作用,即丙球不会参与此次碰撞过程.
甲球与乙球发生的是弹性碰撞,碰撞过程动量守恒,
以向右为正方向,由动量守恒定律得:2mv=2mv甲+mv乙,
由机械能守恒定律得:$\frac{1}{2}$•2mv2=$\frac{1}{2}$•2mv甲2+$\frac{1}{2}$mv乙2,
得:v甲=$\frac{1}{3}$v v乙=$\frac{4}{3}$v (v甲=v v乙=0不合题意,舍去)
然后乙与丙发生碰撞,碰撞过程动量守恒、机械能守恒,
以向右为正方向,由动量守恒定律得:mv乙=mv乙′+mv丙,
由机械能守恒定律得:$\frac{1}{2}$mv乙2=$\frac{1}{2}$mv乙′2+$\frac{1}{2}$mv丙2,解得:v乙′=0 v丙=v乙=$\frac{4}{3}$v,
乙丙碰撞后乙静止,然后加与乙发生二次碰撞,以向右为正方向,
由动量守恒定律得:2mv甲=2mv甲′+mv乙″,
由机械能守恒定律得:$\frac{1}{2}$•2mv甲2=$\frac{1}{2}$•2mv甲′2+$\frac{1}{2}$mv乙″2,
解得:v甲′=$\frac{1}{3}$v甲=$\frac{1}{9}$v v乙″=$\frac{4}{3}$v甲=$\frac{4}{9}$v (v甲=v甲′v乙=0 不合题意,舍去)
答:甲、乙、丙三球最终的速度分别是:$\frac{1}{9}$v、$\frac{4}{9}$v、$\frac{4}{3}$v.
点评 本题考查了碰撞过程中动量守恒定律和机械能守恒的应用,弹性碰撞过程中机械能守恒,分析清楚球的运动过程,应用动量守恒定律与机械能守恒定律即可正确解题,应用动量守恒定律解题时注意正方向的选择.

 阅读快车系列答案
阅读快车系列答案| A. | 布朗运动就是液体分子的运动,它说明了分子在永不停息地做无规则运动 | |
| B. | 密封在容积不变的容器内的气体,若温度升高,则气体分子对器壁单位面积上的平均作用力增大 | |
| C. | 第二类永动机违反了热力学第二定律,所以不可能制成 | |
| D. | 根据热力学第二定律可知,热量能够从高温物体传到低温物体,但不可能从低温物体传到高温物体 |
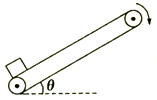 如图所示,足够长的传送带以恒定速率沿顺时针方向运转.现将一个物体轻轻放在传送带底端,物体第一阶段被加速到与传送带具有相同的速度,第二阶段匀速运动到传送带顶端.则下列说法中正确的是( )
如图所示,足够长的传送带以恒定速率沿顺时针方向运转.现将一个物体轻轻放在传送带底端,物体第一阶段被加速到与传送带具有相同的速度,第二阶段匀速运动到传送带顶端.则下列说法中正确的是( )| A. | 第一阶段和第二阶段摩擦力对物体都做正功 | |
| B. | 第一阶段摩擦力对物体做的功大于物体机械能的增加量 | |
| C. | 第二阶段摩擦力对物体做的功等于第二阶段物体机械能的增加量 | |
| D. | 第一阶段摩擦力与物体和传送带间的相对位移的乘积在数值上等于系统产生的内能 |
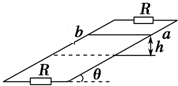 如图所示,两根足够长的固定的平行金属导轨位于倾角θ=30°的斜面上,导轨上、下端各接有阻值R=10Ω的电阻,导轨自身电阻忽略不计,导轨宽度L=2m,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度B=0.5T,质量为m=0.1kg,电阻r=5Ω的金属棒ab在较高处由静止释放,金属棒ab在下滑过程中始终与导轨垂直且与导轨接触良好,当金属棒ab下滑高度h=3m时,速度恰好达到最大值v=2m/s.(g=10m/s2),求:
如图所示,两根足够长的固定的平行金属导轨位于倾角θ=30°的斜面上,导轨上、下端各接有阻值R=10Ω的电阻,导轨自身电阻忽略不计,导轨宽度L=2m,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度B=0.5T,质量为m=0.1kg,电阻r=5Ω的金属棒ab在较高处由静止释放,金属棒ab在下滑过程中始终与导轨垂直且与导轨接触良好,当金属棒ab下滑高度h=3m时,速度恰好达到最大值v=2m/s.(g=10m/s2),求:
 如图所示,质量为1kg的铜块静止于光滑的水平面上,一颗质量为50g的子弹以1000m/s的速度碰到铜块后,又以800m/s的速度被弹回,则此过程中铜块获得的速度大小为90m/s,子弹动量变化量的大小为90kg•m/s.
如图所示,质量为1kg的铜块静止于光滑的水平面上,一颗质量为50g的子弹以1000m/s的速度碰到铜块后,又以800m/s的速度被弹回,则此过程中铜块获得的速度大小为90m/s,子弹动量变化量的大小为90kg•m/s.
 如图是某个做平抛运动物体轨迹的一部分.A、B、C是轨迹上顺次的三个点,A与B、B与C的水平距离均为0.4m,A与B竖直距离为0.25m,B与C竖直距离为0.35m,则此物体的初速度为4m/s,物体经过B点的瞬时速度大小为5m/s,B点距抛出点的水平距离为1.2m.(g=10m/s2)
如图是某个做平抛运动物体轨迹的一部分.A、B、C是轨迹上顺次的三个点,A与B、B与C的水平距离均为0.4m,A与B竖直距离为0.25m,B与C竖直距离为0.35m,则此物体的初速度为4m/s,物体经过B点的瞬时速度大小为5m/s,B点距抛出点的水平距离为1.2m.(g=10m/s2)